Đáp án A
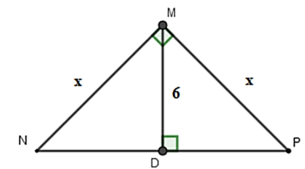
Áp dung hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
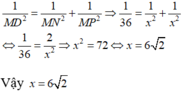
Đáp án A

Áp dung hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
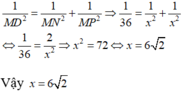
Rút gọn:
a, A = √x√x−6−3√x+6+x36−xxx−6−3x+6+x36−x (đk: x ≥ 0 và x ≠ 36)
b, B = 9−x√x+3−x−6√x+9√x−3−69−xx+3−x−6x+9x−3−6 (đk: x ≥ 0 và x ≠ 9)
c, C = a+b(√a−√b)2−2√ab:(1√a−1√b)2a+b(a−b)2−2ab:(1a−1b)2 (đk: a > 0, b > 0 và a ≠ b)
d, D = (2−a√a2−√a+√a)(2−√a2−a)(2−aa2−a+a)(2−a2−a) (đk: a ≥ 0, a ≠ 2, a ≠ 4)
Bài 1 A) giải hệ phương trình X - 2 y = 7 2 x + y = 1 B) giải phương trình : x² - 6 + 5 = 0 Bài 2 Cho (p) = y = 2x² , (D) y = -x +3 A) vẽ (p) B) tìm tọa độ giao điểm của (p) và (D) bằng phép tính
1. phân tích đa thức thành nhân tử
a)x^2-13
b)x+5√x +6(x≥0)
c)x-4√x +3(x≥0)
d) 3x-6√x -6(x≥0)
2 Tìm GTNN của:
a) A= x-√x +3
b) B=x+3√x +5
c) C=x^4-8xy-x^2y+x^2y^2-xy^2+y^4+2000
Rút gọn biểu thức sau
a/ A=\(\frac{x\sqrt{y}-y\sqrt{x}}{\sqrt{xy}}+\frac{x-y}{\sqrt{x}-\sqrt{y}}\)Với x>0 ; y>0 ;x#y
b/ B=\(\frac{3}{2+\sqrt{3}}+\frac{13}{4-\sqrt{3}}+\frac{6}{\sqrt{3}}\)
c/ C=\(\frac{\sqrt{4-2\sqrt{3}}}{\sqrt{6}-\sqrt{2}}\)
d/ D=\(\left(3\sqrt{2}+\sqrt{6}\right)\sqrt{6-3\sqrt{3}}\)
Bài 1: tìm x. Biết
a. x^2 =49
b. √2x =6
c. 2√x =6
d. √x-1 < √7
Bài 2: tính giá trị của biểu thức
a. √0.04 +√0.16
b. 70.08 + 14√0.36
c. (11- 4√3) . ( 11+ 4√3 )
d. ( 2 - √3 ) . ( 2 +√3 )
Tìm x để biểu thức sau có nghĩa
a) √-2x+3
b) 1+x²
c) √-5/x²+6
d) √x/3
e) √2/x²
1, tính a/ (3+√5)(√10 - √2)√(3-√5)
b/[√2-√(3-√5)].√2
c/(√10 + √6).√(8-2√15)
2, tìm x biết a/ √(x+5)=1+√x
b/√x + √(x-1)=1
c/ √(3-x) + √(x-5)=10
3, phân tích đa thức thành nhân tử:
a/ ab+b√a+√a+1 với a ≥0
b/ x-2√xy + y với x,y ≥ 0
c/√xy + 2√x - 3√y -6 với x,y ≥ 0
4, chứng minh rằng a/ (4+√15).(√10-√6).√(4-√15)=2
b/ √a + √b > √(a+b) (a,b>0)
5, Cho √(8-a) + √(5+a) = 5 tính √[(8-a).(5+a)]
6, rút gọn √(7+2√10)-√15
P/s : mn giúp e với nha
hãy nêu tính đồng biến, nghịch biến của các hàm số bậc nhất sau:
a, y=2x-7
b, y=\(\left(1-\sqrt{2}\right)x+\sqrt{3}\)
c, y=-5x+2
d, y=\(\left(1+m^2\right)x-6\)
e, y=\(y=\left(\sqrt{3}-1\right)x+2\)
f=(2+m^2)x+1
Hãy tính x và y trong mỗi hình sau: (h.6)
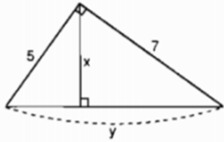
Hình 6