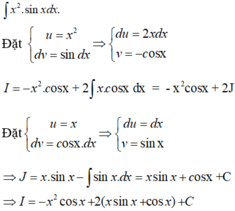Các câu hỏi tương tự
Gỉa sử \(\int\limits^5_3\dfrac{dx}{x^2-x}=aIn5+bIn3+cIn2\times\left(a,b,c\varepsilon Z\right)\) Tính giá trị biểu thức S\(-2a+b+3c^2\)
A. S= 3
B. S= 6
C. S= 0
D. S= -2
Biết
∫
3
4
d
x
(
x
+
1
)
(
x
-
2
)
a
ln
2
+
b
ln
5
+
c
, với a,b,c là...
Đọc tiếp
Biết ∫ 3 4 d x ( x + 1 ) ( x - 2 ) = a ln 2 + b ln 5 + c , với a,b,c là các số hữu tỉ. Tính S = a - 3b + c
A. S = 3
B. S = 2
C. S = -2
D. S = 4
Trong không gian Oxyz, cho điểm Ileft(-2,1,3right) và mặt phẳng left(Pright):2x-y+2z-100. Biết rằng left(Sright) có tâm Ivà cắt left(Pright) theo một đường tròn left(Cright) có chu vi bằng 14pi. Khi đó bán kính rcủa mặt cầu left(Sright) bằng
Đọc tiếp
Trong không gian \(Oxyz\), cho điểm \(I\left(-2,1,3\right)\) và mặt phẳng \(\left(P\right):2x-y+2z-10=0\). Biết rằng \(\left(S\right)\) có tâm \(I\)và cắt \(\left(P\right)\) theo một đường tròn \(\left(C\right)\) có chu vi bằng \(14\pi\). Khi đó bán kính \(r\)của mặt cầu \(\left(S\right)\) bằng
Trong không gian Oxyz, cho hai điểm A (0; 8; 2), B (9; -7; 23) và mặt cầu (S) có phương trình (S): (x - 5)2 + (
y
+
3
)2 + (z + 2)2 72. Mặt phẳng (P): x + by + cz + d 0 đi qua điểm A và tiếp xúc với mặt cầu (S) sao cho khoảng cách từ B đến mặt phẳng (P) lớn nhất. Giá trị của b + c + d khi đó là: A. b + c + d 2 B. b + c + d 4 C. b + c + d 3 D. b + c + d 1
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A (0; 8; 2), B (9; -7; 23) và mặt cầu (S) có phương trình (S): (x - 5)2 + ( y + 3 )2 + (z + 2)2 = 72. Mặt phẳng (P): x + by + cz + d = 0 đi qua điểm A và tiếp xúc với mặt cầu (S) sao cho khoảng cách từ B đến mặt phẳng (P) lớn nhất. Giá trị của b + c + d khi đó là:
A. b + c + d = 2
B. b + c + d = 4
C. b + c + d = 3
D. b + c + d = 1
Trong không gian Oxyz, cho mặt cầu (S):
(
x
-
1
)
2
+
(
y
+
2
)
2
+
(
z
-
3
)
2
48
Gọi...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): ( x - 1 ) 2 + ( y + 2 ) 2 + ( z - 3 ) 2 = 48 Gọi ( α ) là mặt phẳng đi qua hai điểm A(0;0-4), B(2;0;0) và cắt (S) theo giao tuyến là đường tròn (C). Khối nón (N) có đỉnh là tâm của (S), đường tròn đáy là (C) cỏ thể tích lớn nhất bằng
![]()

![]()
Cho hàm số \(y=\dfrac{1}{2}x^4-x^2+m\)(m là tham số ) có đồ thị (Cm), đường tròn (S)có phương trình \(x^2+y^2+2x+6y+1=0\) và điểm A(-1;-6).Tìm m để tồn tại tiếp tuyến với đồ thị (Cm) cắt đường tròn (S) tại hai điểm phân biệt B,C sao cho tam giác ABC có chu vi đạt giá trị lớn nhất
Trong không gian Oxyz cho mặt cầu
(
S
)
:
(
x
-
2
)
2
+
(
y
-
1
)
2
+
(
z
-
1
)
2...
Đọc tiếp
Trong không gian Oxyz cho mặt cầu ( S ) : ( x - 2 ) 2 + ( y - 1 ) 2 + ( z - 1 ) 2 = 9 và điểm M ( a ; b ; c ) ∈ ( S ) sao cho biểu thức P=2a+2b+2c đạt giá trị nhỏ nhất. Tính T=a+b+c.
A. 2
B. 1
C. -2
D. -1
Cho hàm số yf(x) liên tục trên R và thỏa mãn f(x) + f(
π
3
-
x
)
1
2
sin
x
cos
x
(
8
cos
3
x
+
1
)
,
∀
x
∈...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và thỏa mãn f(x) + f( π 3 - x )= 1 2 sin x cos x ( 8 cos 3 x + 1 ) , ∀ x ∈ R Biết tích phân I= ∫ 0 π 3 f ( x ) d x được biểu diễn dưới dạng I= a b ln c d ; a , b , c , d ∈ Z và các phân số a b ; c d là các phân số tối giản. Tính S= a 3 + a b - c + d
![]()
![]()
![]()
![]()
3.Gọi X là tập hợp các điểm trên mặt phẳng .O là một điểm cố định cho trước thuộc X.
Trong tập X ,ta xác định một quan hệ hai ngôi S như sau : MSN <=>OM=ON, M,N\(\in X\)
a. chứng minh S là một quan hệ tương đương trong X
b.xác định lớp tương đương C(A) của một điểmA bất kì thuốc X
Mọi người giúp với ạ.
Trong không gian Oxyz cho hai điểm A(2;-3;2), B(-2;1;4) và mặt cầu
(
S
)
:
(
x
+
1
)
2
+
y
2
+
(
z
-
4
)
2
12
. Điểm M(a,b,c) thuộ...
Đọc tiếp
Trong không gian Oxyz cho hai điểm A(2;-3;2), B(-2;1;4) và mặt cầu ( S ) : ( x + 1 ) 2 + y 2 + ( z - 4 ) 2 = 12 . Điểm M(a,b,c) thuộc mặt cầu (S) sao cho M A → . M B → nhỏ nhất, tính a+b+c
A. 7 3
B. -4
C. 1
D. 4