Chắc đề là: \(\overline{abc}=c^5+20\left(a+b+c\right)\)
Do \(\overline{abc}< 1000\) , nếu \(c\ge4\Rightarrow c^5>1000>\overline{abc}\) (không thỏa mãn)
\(\Rightarrow c< 4\)
TH1: \(c=0\)
\(\Rightarrow10a+b=2\left(a+b\right)\Leftrightarrow8a=b\Rightarrow\left\{{}\begin{matrix}a=1\\b=8\end{matrix}\right.\) \(\Rightarrow\overline{abc}=180\)
TH2: \(c=1\)
\(\Rightarrow100a+10b+1=1+20\left(a+b+1\right)\)
\(\Leftrightarrow8a=b+2\Rightarrow\left\{{}\begin{matrix}a=1\\b=6\end{matrix}\right.\) \(\Rightarrow\overline{abc}=161\)
TH3: \(c=2\)
\(\Rightarrow100a+10b+2=32+20\left(a+b+2\right)\)
\(\Leftrightarrow8a=b+7\Rightarrow\left[{}\begin{matrix}a=1;b=1\\a=2;b=9\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\overline{abc}=112\\\overline{abc}=292\end{matrix}\right.\)
TH4: \(c=3\)
\(\Rightarrow100a+10b+3=243+20\left(a+b+c\right)\)
\(\Leftrightarrow8a=b+30\)
Do \(30\le b+30\le39\Rightarrow b+30=32\Rightarrow\left\{{}\begin{matrix}b=2\\a=4\end{matrix}\right.\)
\(\Rightarrow\overline{abc}=423\)
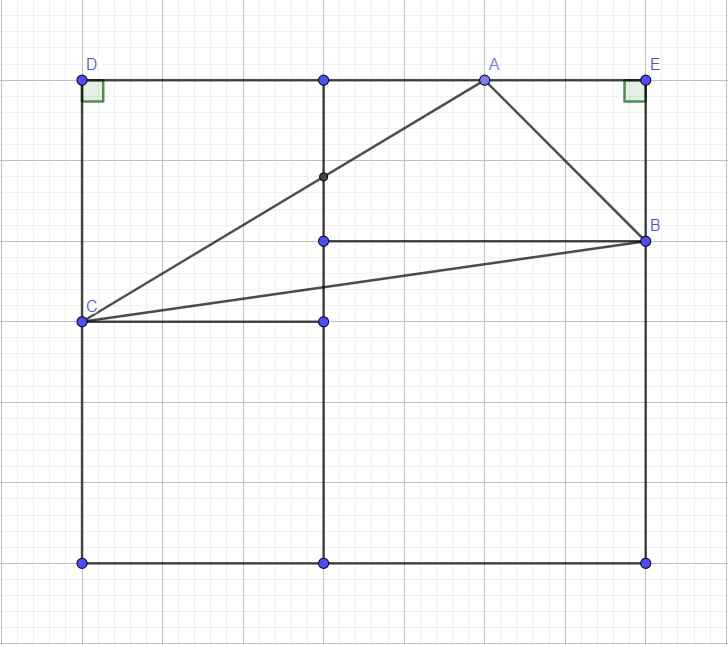
Nhìn hình thì hình vuông chứa điểm C có cạnh \(\dfrac{3a}{2}\) (và phải có số liệu này mới tính được)
Dựng thêm hình vuông (điểm D) và đặt tên các điểm như hình vẽ, trong đó \(CD=\dfrac{3a}{2}\)
\(DE=2a+\dfrac{3a}{2}=\dfrac{7a}{2}\) ; \(AD=a+\dfrac{3a}{2}=\dfrac{5a}{2}\)
\(\Rightarrow S_{BCDE}=\dfrac{1}{2}DE.\left(BE+CD\right)=\dfrac{1}{2}.\dfrac{7a}{2}\left(a+\dfrac{3a}{2}\right)=\dfrac{35a^2}{8}\)
\(S_{ABE}=\dfrac{1}{2}AE.BE=\dfrac{1}{2}a^2\)
\(S_{ADC}=\dfrac{1}{2}AD.CD=\dfrac{1}{2}.\dfrac{5a}{2}.\dfrac{3a}{2}=\dfrac{15a^2}{8}\)
\(\Rightarrow S_{ABC}=S_{BCDE}-\left(S_{ABE}+S_{ADC}\right)=2a^2=...\) em tự thay số