Đặt Tử số là A ta có
\(2A=2+2^2+2^3+2^4+..+2^{2016}\)
\(A=2A-A=2^{2016}-1\)
\(\Rightarrow S=\frac{2^{2016}-1}{1-2^{2016}}=\frac{-\left(1-2^{2016}\right)}{1-2^{2016}}=-1\)
\(S=\frac{1+2+2^2+2^3+...+2^{2015}}{1-2^{2016}}\)
\(\Rightarrow2S=\frac{2\left(1+2+2^2+2^3+...+2^{2015}\right)}{1-2^{2016}}\)
\(\Rightarrow2S=\frac{2+2^2+2^3+2^4+...+2^{2016}}{1-2^{2016}}\)
\(\Rightarrow2S-S=\frac{2+2^2+2^3+2^4+...+2^{2016}}{1-2^{2016}}-\frac{1+2+2^2+2^3+...+2^{2015}}{1-2^{2016}}\)
\(\Rightarrow S=\frac{2^{2016}-1}{1-2^{2016}}=-1\)
Khi nào có bài khó thì cứ đăng lên nhé, mình sẽ giúp ^.^







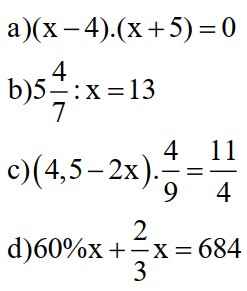 mọi người giúp e với hnay e gặp quá nhiều bài khó nên rất nguy mong mọi người giúp đỡ ạ
mọi người giúp e với hnay e gặp quá nhiều bài khó nên rất nguy mong mọi người giúp đỡ ạ






