Chọn A.
Gọi số phức cần tìm là z = x = yi.
Ta có:
hay x2 + y2 = 25 (*)
Mặt khác: Số phức có phần thực của nó bằng 2 lần phần ảo nên x = 2y
thay vào phương trình (*) ta được: 5y2 = 25 hay 
Vậy số phức cần tìm là: 
Trên mặt phẳng tọa độ tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện:
a) Phần thực của z bằng phần ảo của nó ;
b) Phần thực của z là số đối của phần ảo của nó ;
c) Phần ảo của z bằng hai lần phần thực của nó cộng với 1;
d) Modun của z bằng 1, phần thực của z không âm.
Cho số phức z thỏa mãn 5 z + i = 2 - i z + 1 . Gọi a, b lần lượt là phần thực và phần ảo của số phức 1 + z + z 2 , tổng a+b bằng
A. 13
B. -5
C. 9
D. 5
Trên mặt phẳng tọa độ tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện:
a) Phần thực của z bẳng -2
b) Phần ảo của z bẳng 3
c) Phần thực của z thuộc khoảng (-1;2)
d) Phần ảo của z thuộc đoạn [1;3]
e) Phần thực và phần ảo đều thuộc đoạn [-2; 2]
Số phức z thỏa mãn z - 1 = 5 , 1 z + 1 z ¯ = 5 17 và z có phần ảo dương. Tìm tổng phần thực và phần ảo của z.
Cho số phức z thỏa mãn z = 2 + 1 2 1 - 2 i . Khi đó, tổng bình phương phần thực và phần ảo của z bằng:
A. 18
B. 27
C. 61
D. 72
Tìm tổng phần thực và phần ảo của số phức z thỏa mãn: (1 - i) ( z - 2i) = 2 + i.
A. 4.
B. 3.
C. 5.
D. 7.
Gọi z là số phức có môđun nhỏ nhất và thỏa mãn z + 1 + i = z ¯ + i . Tổng phần thực và phần ảo của số phức z bằng
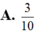
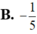
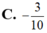
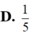
Trên mặt phẳng tọa độ tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện: Phần ảo của z bằng hai lần phần thực của nó cộng với 1
Hãy biểu diễn các số phức z trên mặt phẳng tọa độ, biết |z| ≤ 2 và:
a) Phần thực của z không vượt quá phần ảo của nó;
b) Phần ảo của z lớn hơn 1;
c) Phần ảo của z nhỏ hơn 1, phần thực của z lớn hơn 1.
