Chọn D
Ta có

= 4a + 2b - (a + b) = 3a + b.
Chọn D
Ta có

= 4a + 2b - (a + b) = 3a + b.
Cho a, b là hai số thực đồng thời thỏa mãn b – a – 2 = 0 và 3 a . 2 b = 3 - 2 . Tính b - 5 a
![]()
![]()
![]()
![]()
Cho a,b,c là các số thực thỏa mãn log 2 a + b + c a 2 + b 2 + c 2 + 1 = a a - 2 + b b - 2 + c c - 2 Tìm giá trị lớn nhất của biểu thức P = 3 a + 2 b + c a + b + c
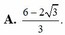
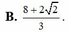
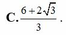
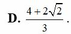
Tìm tham số a, b để hàm số:
y = ( 3 a - 1 ) sin x + b cos x , k h i x < 0 a sin x + ( 3 - 2 b ) cos x , k h i x ≥ 0 l à h à m s ố l ẻ
A.![]()
B. ![]()
C. ![]()
D. ![]()
cho a;b;c > 0, tìm min :
\(P=\dfrac{a}{2b+3c}+\dfrac{b}{2c+3a}+\dfrac{c}{2a+3b}\)
Cho ba số thực dương a,b,c thỏa mãn a 2 + b 2 + c 2 - 2 a + 4 b - 6 c = 10 và a + c=2 . Tính giá trị biểu thức P = 3a + 2b + c khi Q = a 2 + b 2 + c 2 - 14 a - 8 b + 18 c đạt giá trị lớn nhất.
A. 10
B. -10
C. 12
D. -12
Trong không gian Oxyz, cho ba véc tơ a ⇀ ( 5 ; 7 ; 2 ) , b ⇀ ( 3 ; 0 ; 4 ) , c ⇀ ( - 6 ; 1 ; - 1 ) Hãy tìm véc tơ n ⇀ = 3 a ⇀ - 2 b ⇀ + c ⇀ .
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho mặt cầu S : x 2 + y 2 + z 2 - 4 x + 6 y - 3 = 0 và điểm A(2;1;-2). Đường thẳng d đi qua A, tiếp xúc với (S) tại M luôn nằm trên mặt nón (N) cố định. Tọa độ tâm đường tròn đáy của (N) là H(a;b;c). Giá trị 3a-2b+c bằng
A. 8.
B. 4.
C. 2.
D. 6 5 .
Cho hàm số f ( x ) = ln ( 1 - 4 ( 2 x - 1 ) 2 ) . Biết rằng f ( 2 ) + f ( 3 ) + . . . + f ( 2020 ) = ln a b , trong đó a b là phân số tối giản, a , b ∈ N * . Tính b -3a
A. -2
B. 3
C. -1
D. 1
Cho hàm số f ( x ) = ln 1 - 4 ( 2 x - 1 ) 2 . Biết rằng ,f(2) + f(3) + ....+f(2020) = ln a b trong đó a b , là phân số tối giản, a, b ∈ ℕ * . Tính b - 3a
A. -2
B. 3
C. -1
D. 1
Câu 18: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, AA’ = 2a. Tính thể tích khối lăng trụ ABC.A’B’C’ theo a:
\(A,\sqrt{3a^3}\) \(B,\dfrac{\sqrt{3a^3}}{6}\) \(C,\dfrac{\sqrt{3a^3}}{2}\) \(D,2a^3\)