Chia đáy của hình lăng trụ đã cho thành năm tam giác cân có chung đỉnh O là tâm đường tròn ngoại tiếp đáy.
Khi đó diện tích đáy bằng: 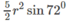
Do đó thể tích lăng trụ đó bằng: 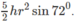
Chia đáy của hình lăng trụ đã cho thành năm tam giác cân có chung đỉnh O là tâm đường tròn ngoại tiếp đáy.
Khi đó diện tích đáy bằng: 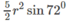
Do đó thể tích lăng trụ đó bằng: 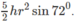
Cho hình trụ (T) có chiều cao h = 2 m , bán kính đáy r = 3 m . Giả sử (L) là hình lăng trụ đều n cạnh có hai đáy là đa giác đều nội tiếp đường tròn đáy của hình trụ (T). Khi n tăng lên vô hạn thì tổng diện tích tất cả các mặt của của khối lăng trụ (L) (tính bằng m 2 ) có giới hạn là:
![]()
![]()
![]()
![]()
Cho hình trụ có đường cao h và bán kính đáy là r. Trong các khối lăng trụ tứ giác nội tiếp hình trụ thì khối lăng trụ có thể tích lớn nhất bằng:
A. h r 2
B. 2h r 2
C. 3h r 2
D. 4h r 2
Cho hình trụ có bán kính đáy bằng a và chiều cao bằng h. Tính thể tích V của khối lăng trụ tam giác đều nội tiếp hình trụ đã cho
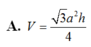
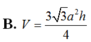
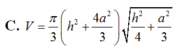
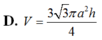
Một hình trụ có bán kính đáy bằng R và thiết diện qua trục là hình vuông. Tính thể tích V của khối lăng trụ tứ giác đều nội tiếp hình trụ.
![]()
![]()
![]()
![]()
Một hình trụ có bán kính đáy bằng R và thiết diện đi qua trục là hình vuông. Tính thể tích V của khối lăng trụ tứ giác đều nội tiếp hình trụ.
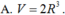
![]()
![]()
![]()
Một hình trụ có bán kính đáy bằng R và thiết diện đi qua trục là hình vuông. Tính thể tích V của khối lăng trụ tứ giác đều nội tiếp hình trụ.
![]()
![]()
![]()
![]()
Một khối trụ có đường kính đáy bằng chiều cao và nội tiếp trong mặt cầu bán kính R thì thể tích của khối trụ là:
A. 2 π R 3
B. π R 3 2 2
C. π R 3 2 6
D. 2 3 π R 3
Cho lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a và có đường cao h. Một hình trụ có các đường tròn đáy tiếp xúc với các cạnh của tam giác đáy được gọi là hình trụ nội tiếp trong lăng trụ. Hãy tính diện tích xung quanh của hình trụ nội tiếp đó.
Cho hình nón tròn xoay (H) đỉnh S, đáy là hình tròn bán kính R, chiều cao bằng h. Gọi (H') là hình trụ tròn xoay có đáy là hình tròn bán kính r (0 < r < R) nội tiếp (H). Tính tỉ số thể tích của (H') và (H)