Đáp án B
Gọi H là chân đường cao kẻ từ S đến DC, K là chân đường cao kẻ từ S đến (ABCD). Khi đó ta dễ dàng tính được: . Lại có:
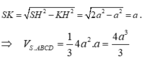
=> Chọn phương án B.
Đáp án B

Gọi H là chân đường cao kẻ từ S đến DC, K là chân đường cao kẻ từ S đến (ABCD). Khi đó ta dễ dàng tính được: . Lại có:
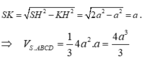
=> Chọn phương án B.
Tính thể tích V của khối chóp đều S.ABC có cạnh đáy bằng 2a và cạnh bên bằng a 3
A . V = a 3 3
B . V = a 3 5 3
C . V = a 3 5
D . V = a 3 3 3
Cho khối chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh bằng a, tâm O cạnh bên bằng a 3 . Gọi M là trung điểm của CD, H là điểm đối xứng của O qua SM (tham khảo hình vẽ bên). Thể tích khối đa diện ABCDSH bằng
A. a 3 10 12
B. a 3 10 18
C. a 3 10 24
D. 5 a 3 10 24
Bài 10. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, cạnh bên bằng a * sqrt(3) . O là tâm hình vuông 1/ Chứng minh :a) (SAC) I (ABCD) b) (SAC) (SBD). 2 / a ) Tính d(S; (ABCD)) b) Tính d(O; (SCD)) 3/ Tính góc giữa:a) SC và (ABCD); b) (SAB) và (ABCD).
Cho hình chóp tứ giác có đáy ABCD là hình chữ nhật có AB = a; AD = 2a, cạnh bên SA vuông góc với mặt phẳng đáy và SA = a 2 . Thể tích V của khối chóp là :
A . V = 2 2 9 a 3
B . V = 2 3 a 3
C . V = 2 2 a 3
D . V = 2 2 3 a 3
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh AB = a (a > 0). Góc giữa mặt bên và mặt đáy bằng 60 0 . Tính thể tích khối chóp S.ABCD:
A . a 3 3 2
B . a 3 6
C . a 3 3 3
D . a 3 3 6
Cho khối chóp tứ giác đều S.ABCD có cạnh bằng a, cạnh bên SC tạo với mặt đáy một góc 45 0 .Tính thể tích của khối chóp S. ABCD
A . V = 2 a 3 3
B . V = 2 a 3 6
C . V = 2 a 3 3
D . V = 2 a 3
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 60 0 . Tính thể tích khối chóp S.ABCD
A. a 3 6 2
B. a 3 6 6
C. a 3 6
D. a 3 6 3
Cho khối chóp tứ giác đều có cạnh đáy bằng a và cạnh bên bằng a 3 Tính thể tích V của khối chóp đó theo a:
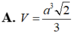
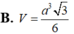
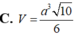
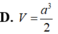
Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng a, SA = 3 . Tính thể tích V của khối chóp S.ABC
A . V = 35 a 3 24
B . V = 3 a 3 6
C . V = 2 a 3 6
D . V = 2 a 3 2