Question

Tính số đo $x$ trong hình vẽ sau:

Answer 1

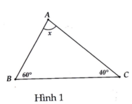
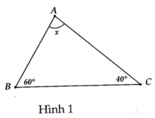
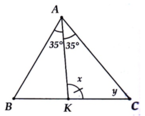
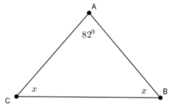
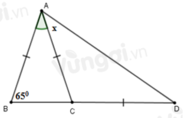
Xét Tam giác `ABC: AB = AC`

`-> \text {Tam giác ABC cân tại A}`

`->`\(\widehat{B}=\widehat{C}=65^0\)

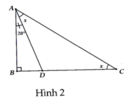
Ta có: \(\widehat{ACB}+\widehat{ACD}=180^0 (\text {2 góc kề bù})\)

`->`\(65^0+\widehat{ACD}=180^0\)

`->`\(\widehat{ACD}=115^0\)

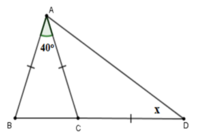
Xét Tam giác `ACD: CA = CD`

`-> \text {Tam giác ACD cân tại C}`

`->` \(\widehat{A}=\widehat{D}\)

Xét Tam giác `ACD:`

\(\widehat{CAD}+\widehat{CDA}+\widehat{ACD}=180^0 (\text {đlí tổng 3 góc trong 1 tam giác})\)

`->`\(\widehat{CAD}+\widehat{CDA}+115^0=180^0\)

`->`\(\widehat{CAD}+\widehat{CDA}=65^0\)

Mà \(\widehat{CAD}=\widehat{CDA}\)

`->`\(\widehat{CAD}=\widehat{CDA}=\) `65/2=32,5^0`