Các câu hỏi tương tự
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
Cho hàm số
y
sin
x
-
1
x
2
-
4
có đồ thị (C). Có bao nhiêu khẳng định dưới đây là đúng? (*) x 2 là một TCĐ (*) x -2 là một TCĐ (*) TXĐ: Dy [l,+¥) (*) y 0 là một TCN (*) TXĐ: Dy R{± 2} ...
Đọc tiếp
Cho hàm số y = sin x - 1 x 2 - 4 có đồ thị (C). Có bao nhiêu khẳng định dưới đây là đúng?
(*) x = 2 là một TCĐ
(*) x = -2 là một TCĐ
(*) TXĐ: Dy = [l,+¥)
(*) y = 0 là một TCN
(*) TXĐ: Dy = R\{± 2}
(*) TXĐ: Dy = [1, +¥)\{2}
A. 2
B. 3
C. 4
D. 5
Hình chóp tam giác đều S.ABC. Hạ
S
H
⊥
A
B
C
. Biết S(l; 0; 2); A(3; 4; 4); H(1; 1; 1). Tính bán kính R mặt cầu ngoại tiếp S.ABC
Đọc tiếp
Hình chóp tam giác đều S.ABC. Hạ S H ⊥ A B C . Biết S(l; 0; 2); A(3; 4; 4); H(1; 1; 1). Tính bán kính R mặt cầu ngoại tiếp S.ABC
![]()
![]()
![]()
![]()
Tìm x, biết log 2 x = -2
A. x = -4 B. x = 1/4
C. x = -1/4 D. x = 4
Tìm x, biết log 2 x = -2
A. x = -4 B. x = 1/4
C. x = -1/4 D. x = 4
Tìm x, biết log 3 x + log 4 x + 1 = 2
A. x = 1 B. x = 2
C. x = 3 D. x = 4
Tìm x, biết log 3 x + log 4 ( x + 1 ) = 2
A. x = 1 B. x = 2
C. x = 3 D. x = 4
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(0; 1; 2) và B(2;-l;4). Phương trình mặt cầu đường kính AB là
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(0; 1; 2) và B(2;-l;4). Phương trình mặt cầu đường kính AB là
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(0; 1; 2) và B(2;-l;4). Phương trình mặt cầu đường kính AB là
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(0; 1; 2) và B(2;-l;4). Phương trình mặt cầu đường kính AB là
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(0;-2;-l), B(-2;-4;3), C(l;3;-l) và mặt phẳng (P): x+y-2z-30 . Tìm điểm
M
∈
(
P
)
sao cho
|
M
A
+
M
B
⇀
+
2
M
C
⇀
|
đạt giá trị nhỏ nhất.
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(0;-2;-l), B(-2;-4;3), C(l;3;-l) và mặt phẳng (P): x+y-2z-3=0 . Tìm điểm M ∈ ( P ) sao cho | M A + M B ⇀ + 2 M C ⇀ | đạt giá trị nhỏ nhất.
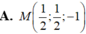

![]()
![]()





