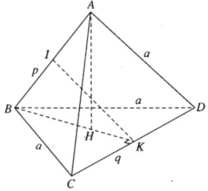
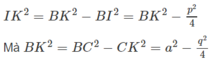
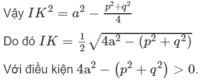
Gọi I và K lần lượt là trung điểm của AB và CD (h.3.80), ta có IK là đoạn vuông góc chung của AB và CD và độ dài đoạn IK là khoảng cách cần tìm:
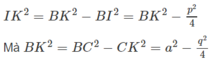
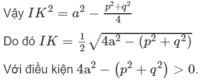
Cho tứ diện ABCD có AB = 2, AC =3, AD =BC = 4, B D = 2 5 , CD = 5. Khoảng cách giữa hai đường thẳng AC và BD gần nhất với giá trị nào sau đây.
A. 4
B. 1
C. 2
D. 3
Chứng minh rằng nếu đường thẳng nối trung điểm hai cạnh AB và CD của tứ diện ABCD là đường vuông góc chung của AB và CD thì AC = BD và AD = BC.
Cho tứ diện ABCD có AB=AD= a 2 , BC=BD=a, CA=CD=x. Khoảng cách từ B đến mặt phẳng (ACD) bằng a 3 2 . Biết thể tích của khối tứ diện bằng a 3 3 12 . Góc giữa hai mặt phẳng (ACD) và (BCD) là
A. 60 o
B. 45 o
C. 90 o
D. 120 o
Cho hình tứ diện ABCD. Gọi M , N lần lượt là trung điểm các cạnh AB và CD. Biết AB=CD=AN=BN=CM=MD =a (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng AB và CD bằng
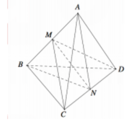
A. a 3 3
B. a 3 2
C. a 3 6
D. a 2 2
Cho tứ diện đều ABCD cạnh a. Tính khoảng cách giữa hai đường thẳng AB và CD
A. a 2
B. a 2
C. a
D. a 2 2
Cho tứ diện ABCD với G là trọng tâm và các điểm M, N, P, Q, I, J lần lượt là trung điểm của các cạnh AB, BC, CD, AD, AC, BD.
A B → + A C → + A D → bằng:
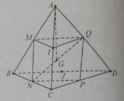
A. 4 A G →
B. 2 A G →
C. A G →
D. 1 / 2 A G →
Cho tứ diện ABCD có BC = CD = BD = 2a, AC = AD = 2 , AB = a. Góc giữa hai mặt phẳng (ACD) và (BCD) có số đo là:
A. 90 o .
B. 60 o .
C. 45 o
D. 30 o
b1: cho hình hộp ABCDA'B'C'D' có tất cả các mặt đều là hinh fthoi cạnh a. góc BAA'= góc BAD = góc DAA' = 60 độ. tính độ dài AC
b2: cho tứ diện ABCD có CD=z/2 AB. I,J,K lần lượt là trung điểm của BC,AC,BD. biết JK=5/6AB. tính góc giữa CD với Ị và AB
