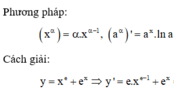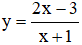Các câu hỏi tương tự
Cho hai hàm số
f
x
ax
4
+
bx
3
+
cx
2
+
dx
+
e
và
g
x
mx
3
+
nx
2
+
px
+
1
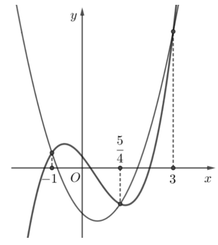
với a, b, c, d, e, m, n, plà các số thực. Đồ thị của hai hàm số y f(x), y g(x) như hình vẽ bên. Tổng các nghiệm của phương trình f(x) + q g(x) + e bằn...
Đọc tiếp
Cho hai hàm số f x = ax 4 + bx 3 + cx 2 + dx + e và g x = mx 3 + nx 2 + px + 1 với a, b, c, d, e, m, n, plà các số thực. Đồ thị của hai hàm số y = f'(x), y = g'(x) như hình vẽ bên. Tổng các nghiệm của phương trình f(x) + q= g(x) + e bằng
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
Cho hàm số y f(x) liên tục trên khoảng
0
;
+
∞
. Biết f(1) 1 và f(x) xf(x) + ln (x). Giá trị f(e) bằng A. e B. 1 C. 2 D.
1
e
Đọc tiếp
Cho hàm số y = f(x) liên tục trên khoảng 0 ; + ∞ . Biết f(1) = 1 và f(x) = xf'(x) + ln (x). Giá trị f(e) bằng
A. e
B. 1
C. 2
D. 1 e
Cho hàm số f(x) có đạo hàm f(x) liên tục trên đoạn [1;e] thỏa mãn
f
1
1
2
và
x
.
f
x
xf
2
x
-
3...
Đọc tiếp
Cho hàm số f(x) có đạo hàm f'(x) liên tục trên đoạn [1;e] thỏa mãn f 1 = 1 2 và x . f ' x = xf 2 x - 3 f x + 1 x , ∀ x ∈ 1 ; e . Giá trị của f(e) bằng
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Câu 1. Đường thẳng nào cho dưới đây là tiệm cận ngang của đồ thị hàm số A. y -2 B. y -1 C. x 2 D. y 2Câu 2. Cho hàm số f(x) x2lnx. Tính f(e) A. 3e B. 2e C. e D. 2 + eCâu 3. Viết công thức tính V của khối cầu có bán kính r. Câu 4. Thể tích khối chóp tứ giác đều có tất cả các cạnh bằng 6 gần bằng số nào sau đây nhất? A. 48 B. 46 C. 52 D. 51Câu 5. Tìm tập xác định D của hàm số y ln(x2 - 3x) A. D (0;3) B. D [0;3] C. D (-∞;0)∪(3;+∞) D. D (-∞;0)∪[3;+∞)
Đọc tiếp
Câu 1. Đường thẳng nào cho dưới đây là tiệm cận ngang của đồ thị hàm số
A. y = -2
B. y = -1
C. x = 2
D. y = 2
Câu 2. Cho hàm số f(x) = x2lnx. Tính f'(e)
A. 3e
B. 2e
C. e
D. 2 + e
Câu 3. Viết công thức tính V của khối cầu có bán kính r.
Câu 4. Thể tích khối chóp tứ giác đều có tất cả các cạnh bằng 6 gần bằng số nào sau đây nhất?
A. 48
B. 46
C. 52
D. 51
Câu 5. Tìm tập xác định D của hàm số y = ln(x2 - 3x)
A. D = (0;3)
B. D = [0;3]
C. D = (-∞;0)∪(3;+∞)
D. D = (-∞;0)∪[3;+∞)
Đạo hàm của hàm số
y
e
x
-
e
-
x
là: A.
y
e
x
+
e
-
x
2
x...
Đọc tiếp
Đạo hàm của hàm số y = e x - e - x là:
A. y ' = e x + e - x 2 x
B. y ' = e x - e - x 2 x
C. y ' = e x - e - x x
D. y ' = e x + e - x x
Cho hàm số y f(x) có đạo hàm liên tục trên khoảng thỏa mãn
x
2
f
x
+
f
x
0
và
f
x
≠
0
,
∀...
Đọc tiếp
Cho hàm số y= f(x) có đạo hàm liên tục trên khoảng ![]() thỏa mãn
x
2
f
'
x
+
f
x
=
0
và
f
x
≠
0
,
∀
x
∈
0
;
+
∞
. Tính f(2) biết f(1) = e.
thỏa mãn
x
2
f
'
x
+
f
x
=
0
và
f
x
≠
0
,
∀
x
∈
0
;
+
∞
. Tính f(2) biết f(1) = e.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số y f(x) xác định và liên tục trên [ a; e] và có đồ thị hàm số y f’ (x) như hình vẽ bên. Biết rằng f(a) + f( c)) f( b) + f( d) . Tìm giá trị lớn nhất và nhỏ nhất của hàm số y f( x) trên [ a; e]? A.
m
a
x
[
a
,...
Đọc tiếp
Cho hàm số y= f(x) xác định và liên tục trên [ a; e] và có đồ thị hàm số y= f’ (x) như hình vẽ bên. Biết rằng f(a) + f( c)) = f( b) + f( d) . Tìm giá trị lớn nhất và nhỏ nhất của hàm số y= f( x) trên [ a; e]?
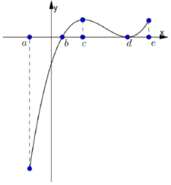
A. m a x [ a , e ] f ( x ) = f ( c ) m i n [ a , e ] f ( x ) = f ( a )
B. m a x [ a , e ] f ( x ) = f ( a ) m i n [ a , e ] f ( x ) = f ( b )
C. m a x [ a , e ] f ( x ) = f ( e ) m i n [ a , e ] f ( x ) = f ( b )
D. m a x [ a , e ] f ( x ) = f ( d ) m i n [ a , e ] f ( x ) = f ( b )
Giả sử hàm số f(x) (ax2 + bx + c).e–x là một nguyên hàm của hàm số g(x) x(1 – x).e–x. Giá trị của biểu thức A a + 2b + 3c bằng A. 6 B. 4 C. 9 D. 3
Đọc tiếp
Giả sử hàm số f(x) = (ax2 + bx + c).e–x là một nguyên hàm của hàm số g(x) = x(1 – x).e–x. Giá trị của biểu thức A = a + 2b + 3c bằng
A. 6
B. 4
C. 9
D. 3
Diện tích hình phẳng được giới hạn bởi các đường y ln x, x 1/e, x e và trục hoành là A.
1
-
1
e
B.
2
1
+
1
e
C.
2
1
-
1...
Đọc tiếp
Diện tích hình phẳng được giới hạn bởi các đường y = ln x, x = 1/e, x = e và trục hoành là
A. 1 - 1 e
B. 2 1 + 1 e
C. 2 1 - 1 e
D. 1 + 1 e