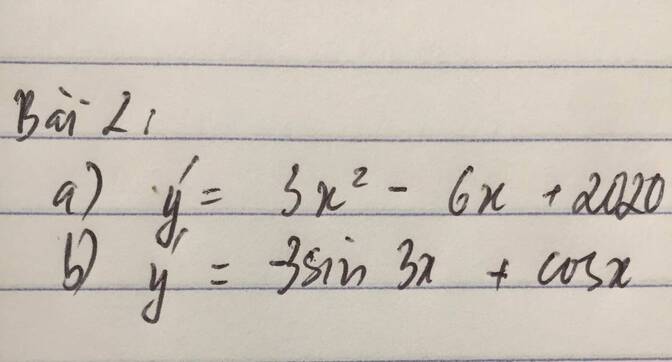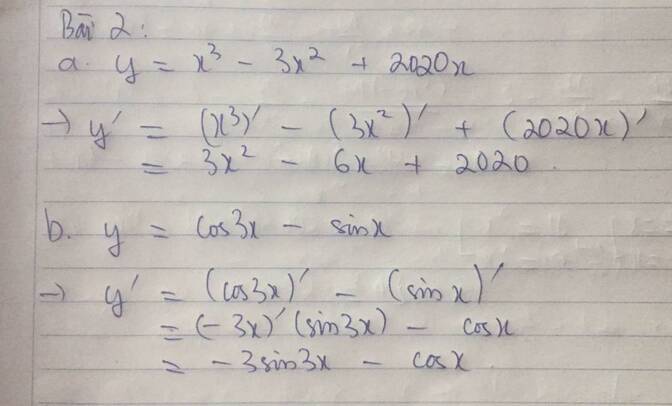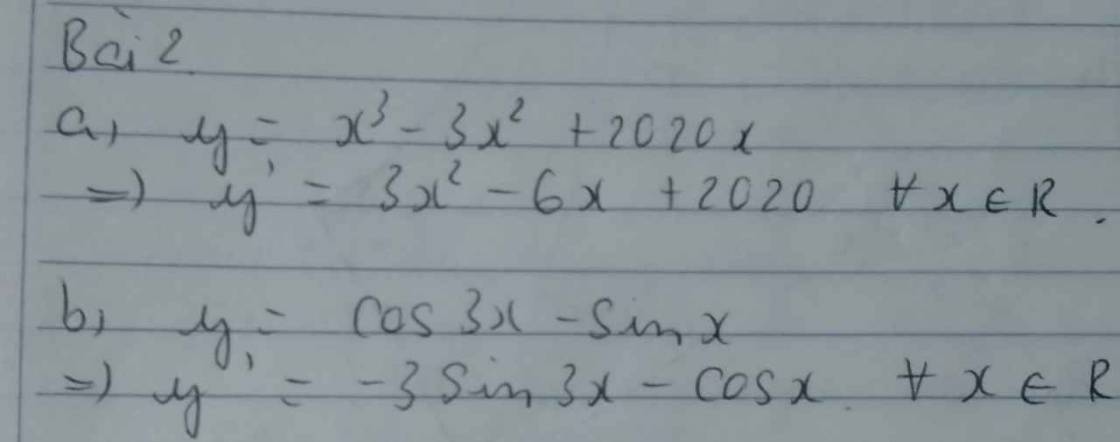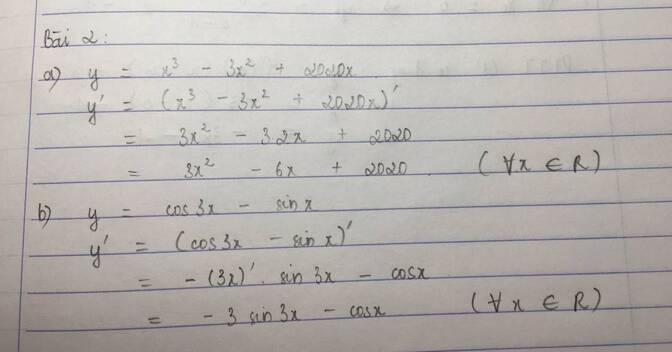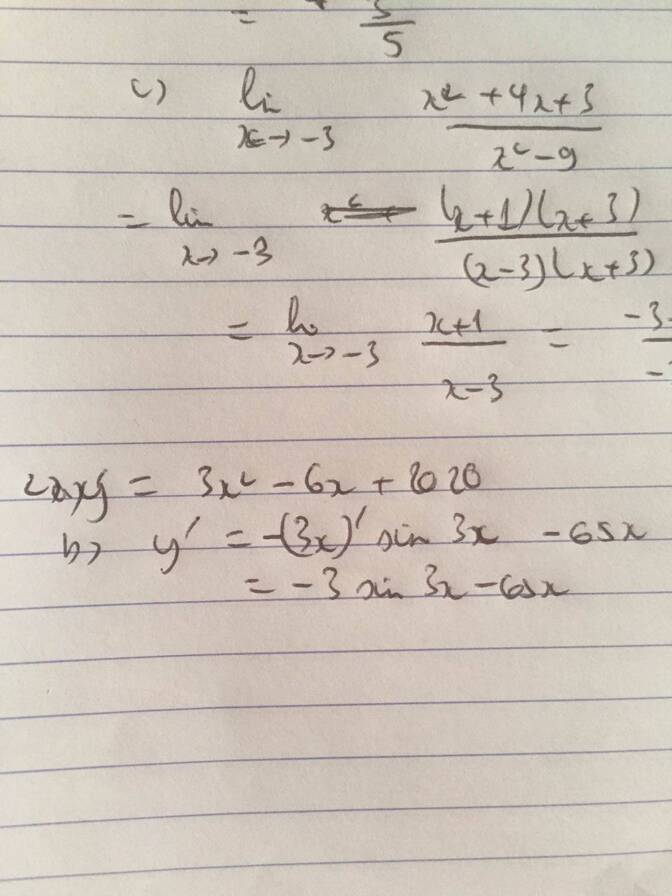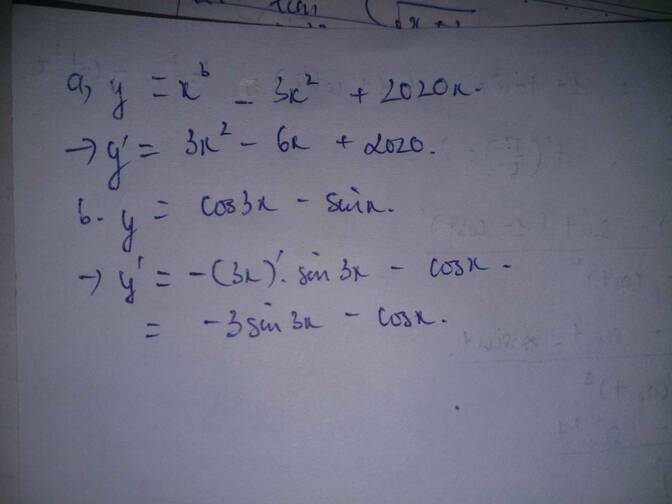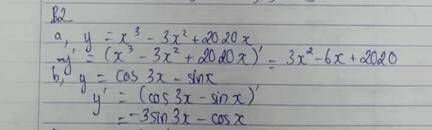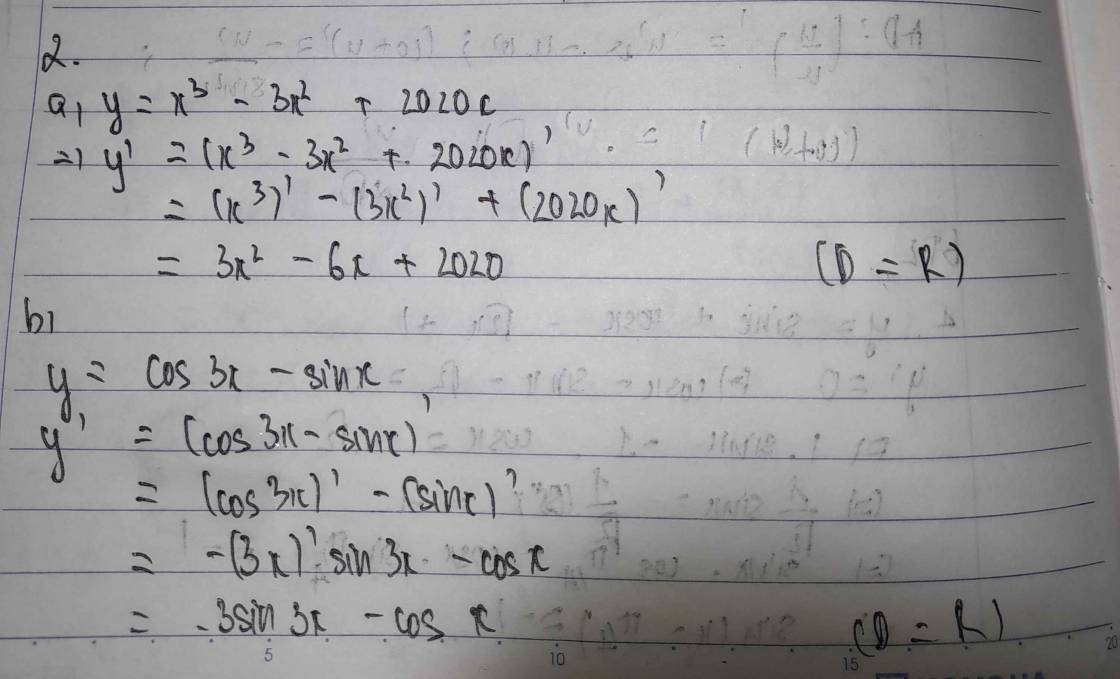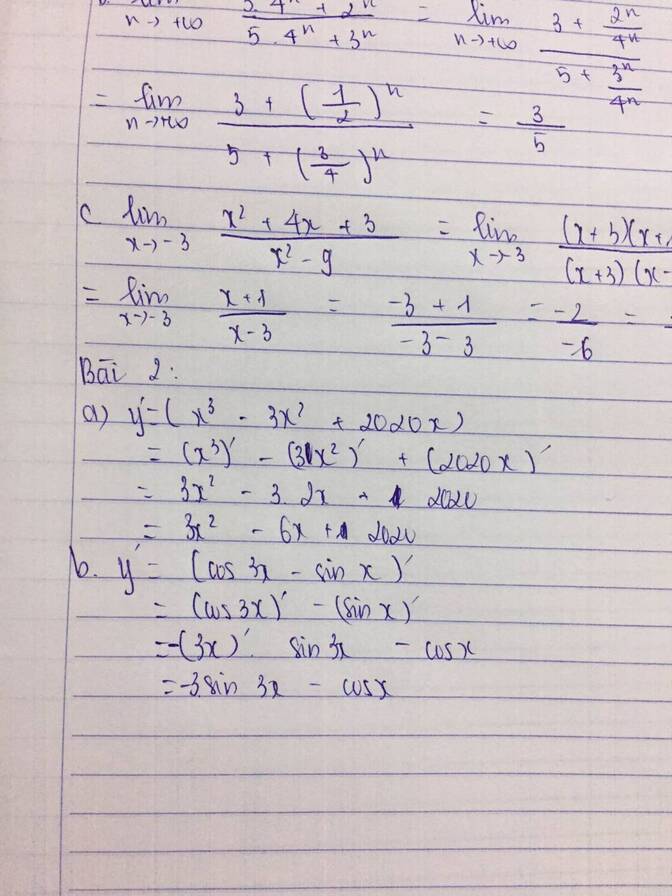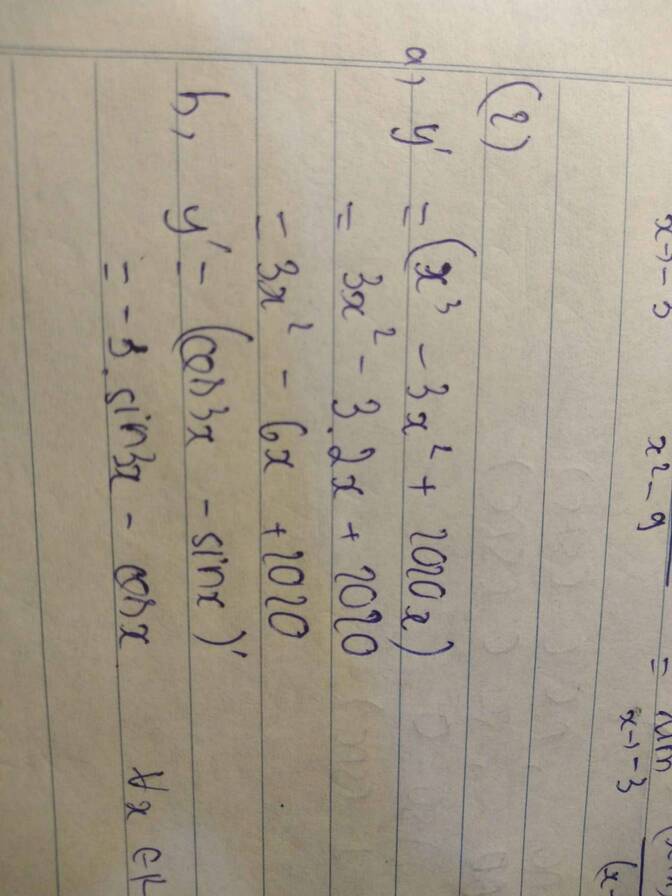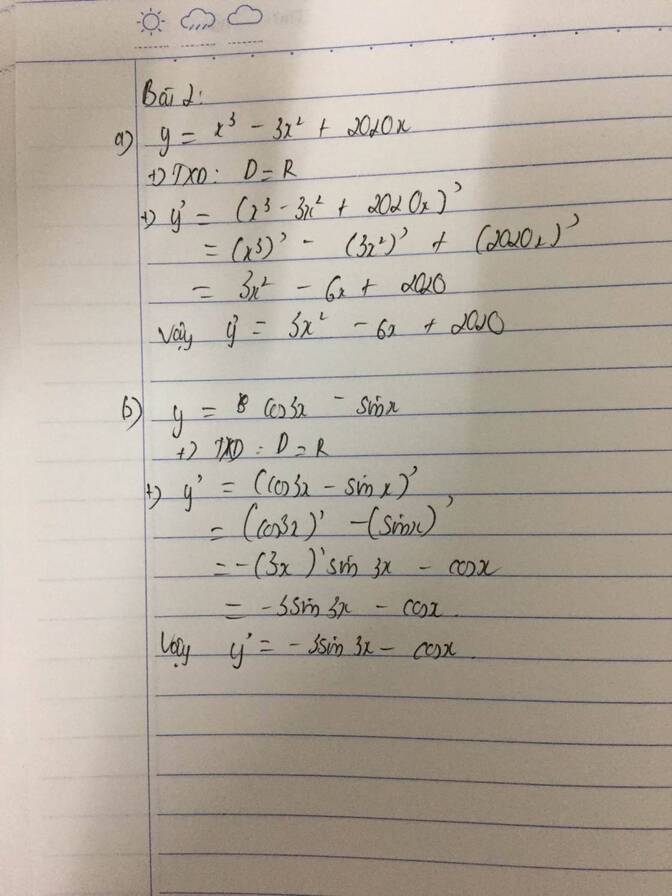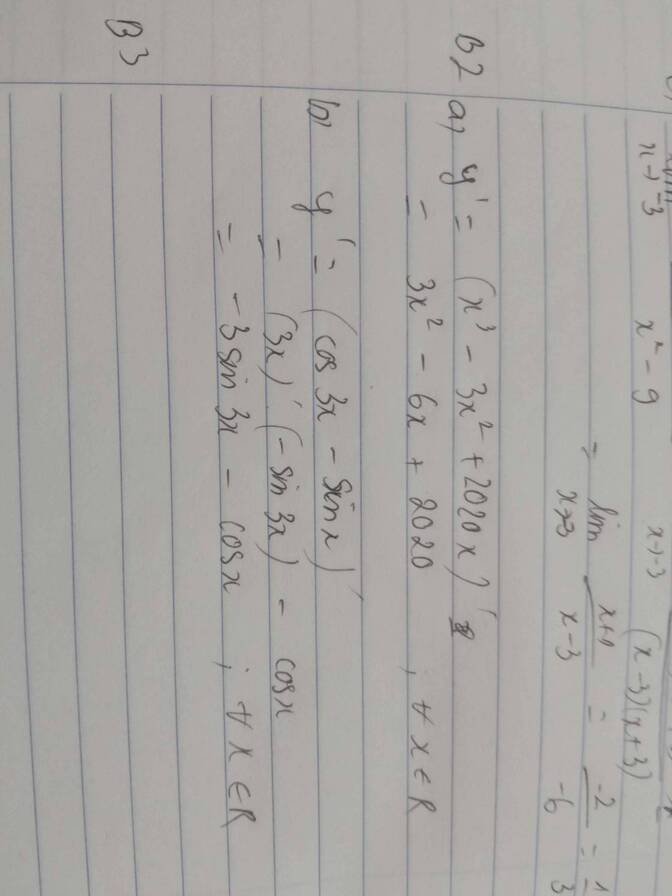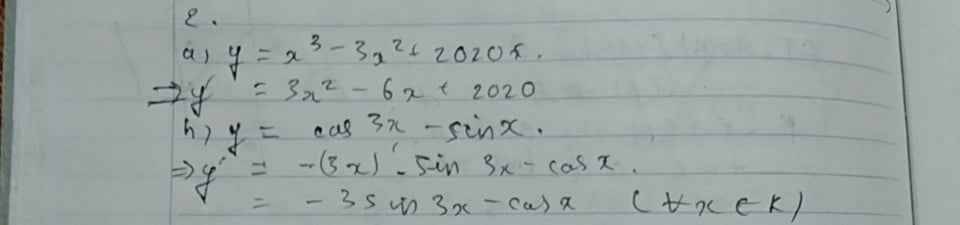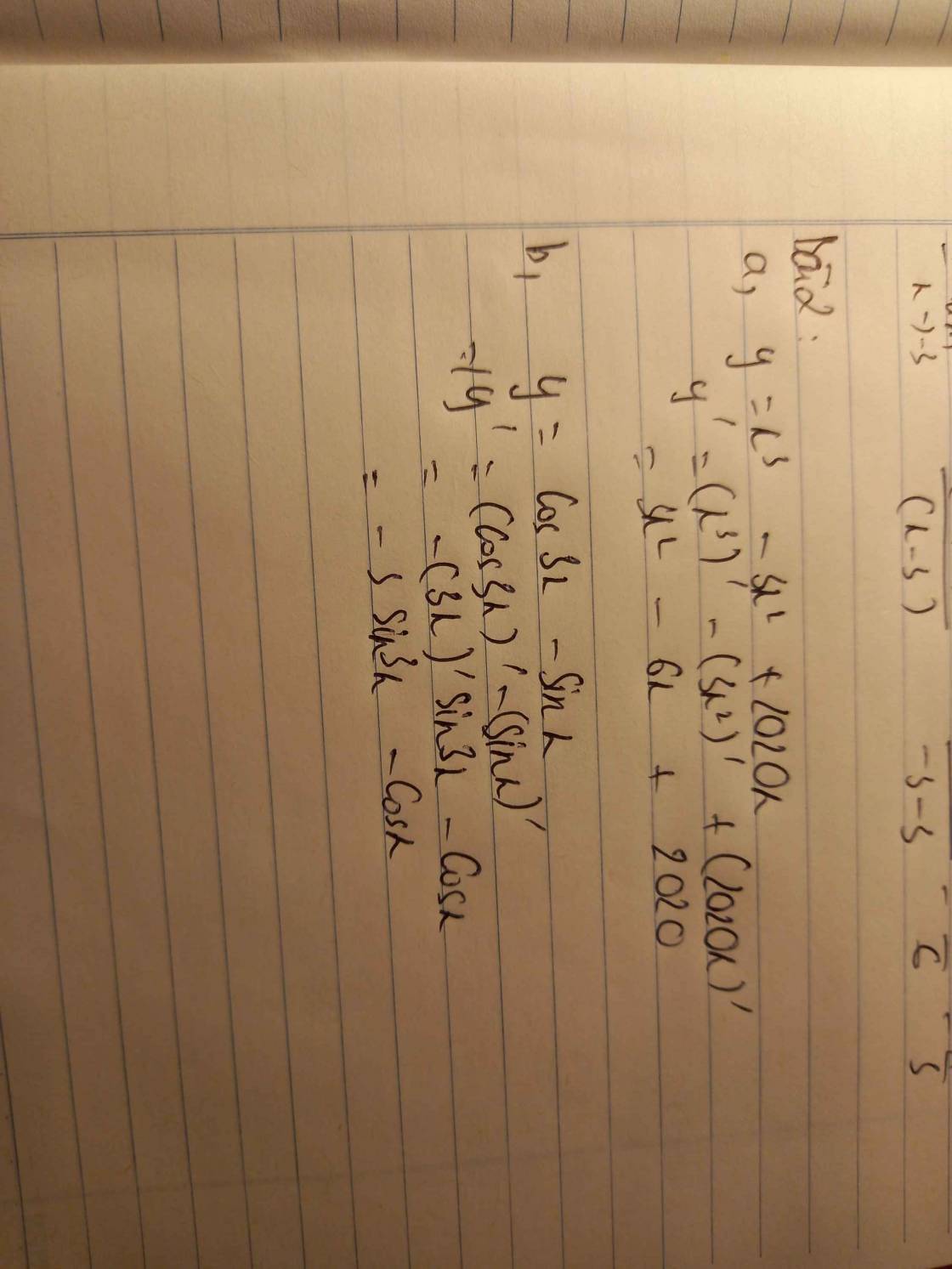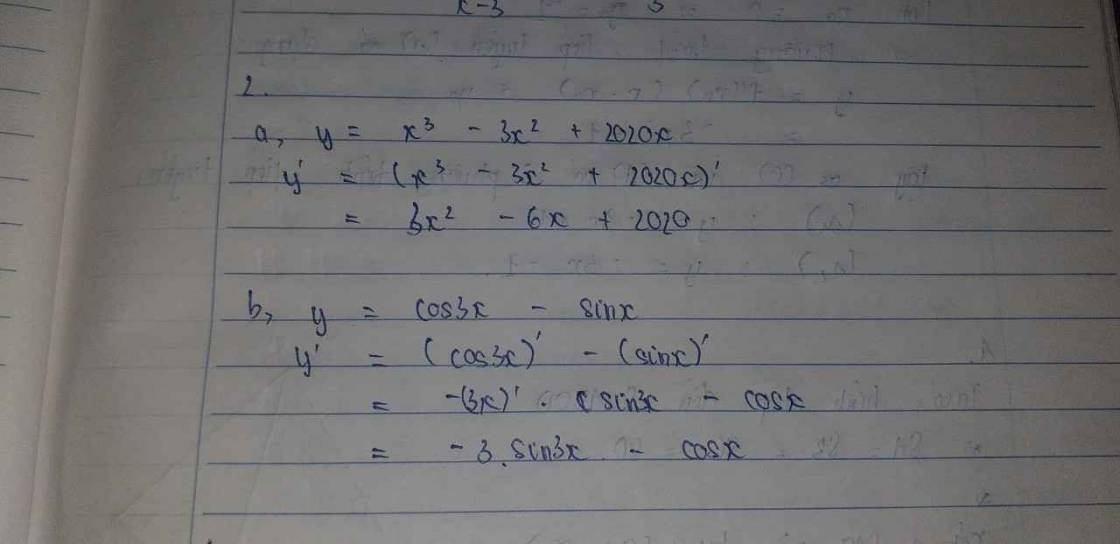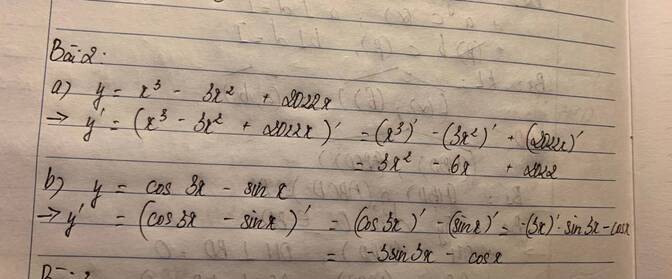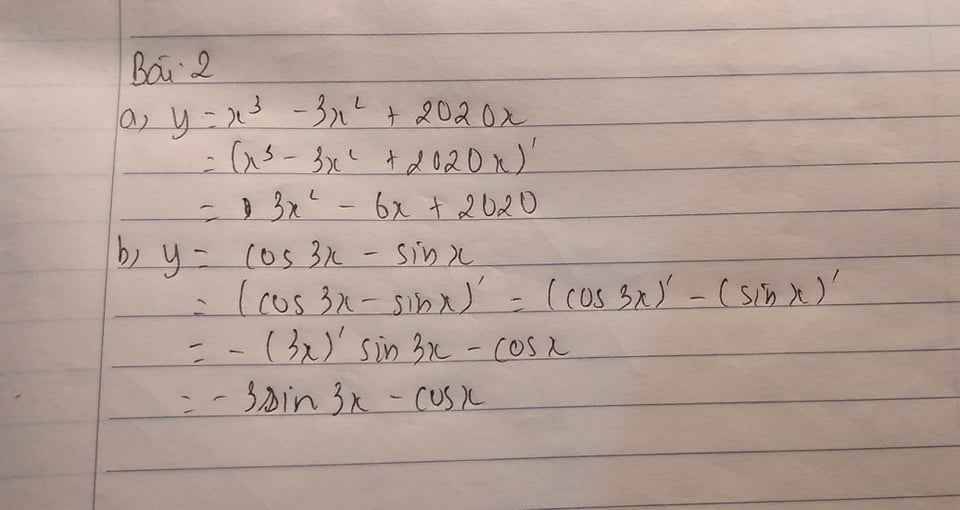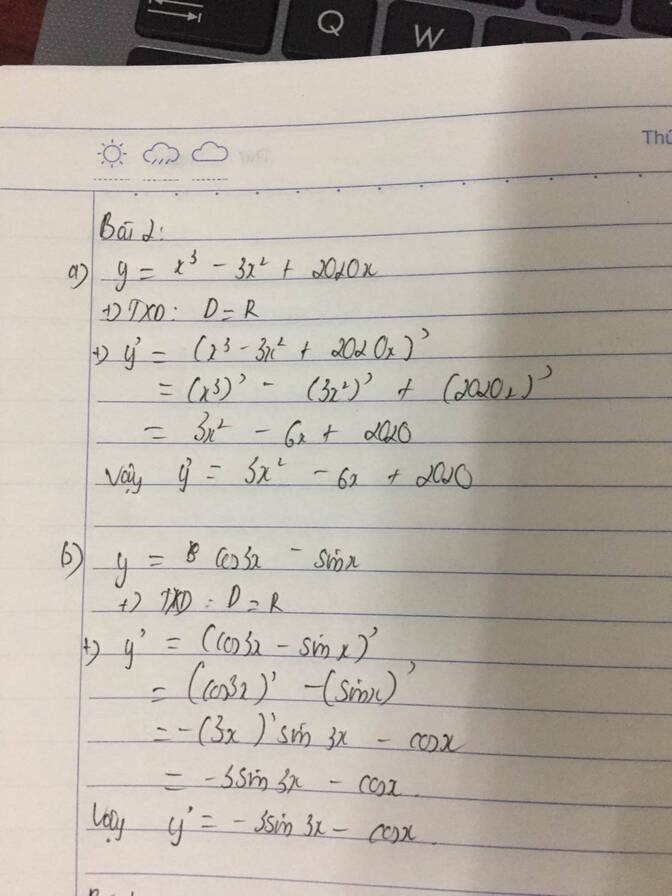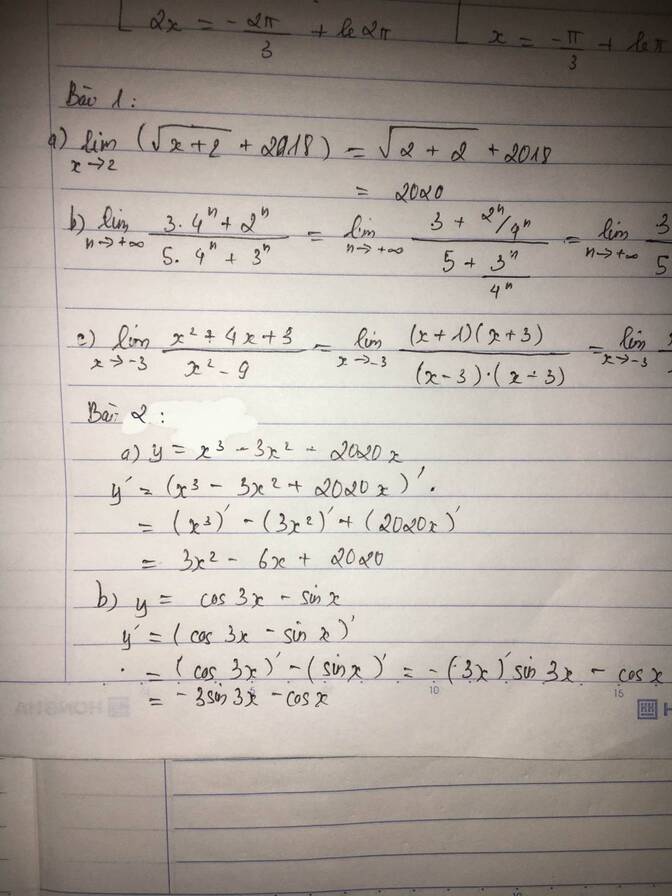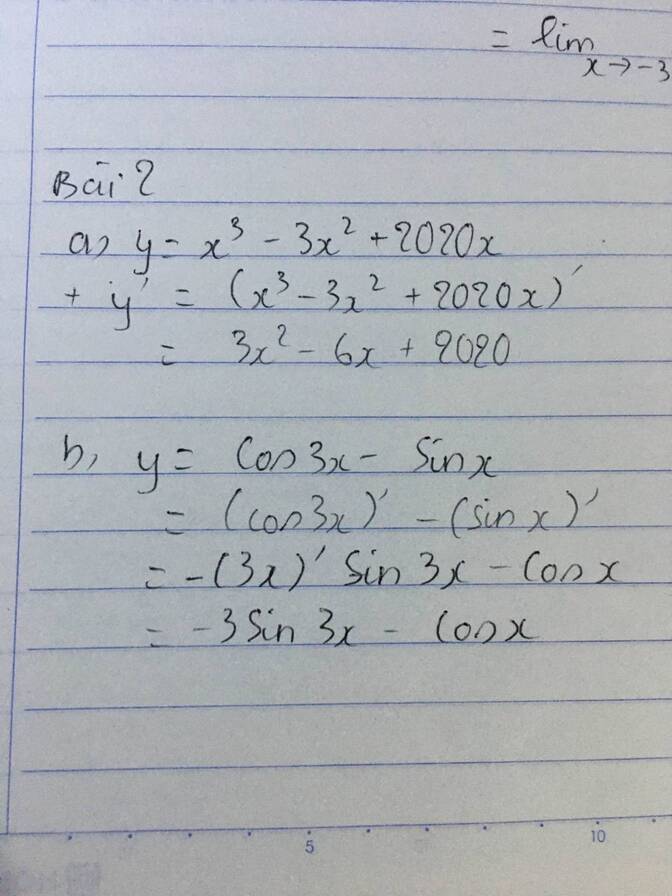Question

Tính đạo hàm các hàm số sau:

a) $y={{x}^{3}}-3{{x}^{2}}+2020x$.

b) $y=\cos 3x-\sin x$.

Answer 1

  

Answer 2

a) \(y'=3x^2-6x+2020\)

b) \(D=ℝ\)

\(\Rightarrow y'=\left(cos3x-sinx\right)'=-3sin3x-cosx\)

Answer 3

    

Answer 4

a) y=x3−3x2+2020xy=x3−3x2+2020x.

+ Tập xác định: D=RD=R.

+ y′=(x3−3x2+2020x)′y′=(x3−3x2+2020x)′=(x3)′−(3x2)′+(2020x)′=(x3)′−(3x2)′+(2020x)′=3x2−6x+2020=3x2−6x+2020.

+ Vậy y′=3x2−6x+2020y′=3x2−6x+2020.

b) y=cos3x−sinxy=cos⁡3x−sin⁡x.

+ Tập xác định: D=RD=R.

+ y′=(cos3x−sinx)′y′=(cos⁡3x−sin⁡x)′=(cos3x)′−(sinx)′=(cos⁡3x)′−(sin⁡x)′=−(3x)′sin3x−cosx=−(3x)′sin⁡3x−cos⁡x=−3sin3x−cosx=−3sin⁡3x−cos⁡x.

+ Vậy y′=−3sin3x−cosxy′=−3sin⁡3x−cos⁡x.

Answer 5

Answer 6

  

Answer 7

  

Answer 8

  

Answer 9

a)

y′=3x2−6x+2020y′=3x2−6x+2020.  

b)

  y′=−3sin3x−cosxy′=−3sin⁡3x−cos⁡x.

Answer 10

  

Answer 11

  

Answer 12

  

Answer 13

  

Answer 14

Answer 15

  

Answer 16

  

Answer 17

a, y'=3x²-6x+2020 ∀xϵR
b, y'=-sin3x.(3x)'-cosx=-3sin3x-cosx ∀xϵR

 

Answer 18

  

Answer 19

  

Answer 20

Answer 21

Answer 22

Answer 23

  

Answer 24

Answer 25

Answer 26

  

Answer 27

a)

\(=\left(x^3\right)`-\left(3x^2\right)`+\left(2022x\right)`=3x^2-6x+2022\)

b)

\(\left(cos3x\right)`-\left(sinx\right)`=-\left(3x\right)`sin3x-cosx=-3sin3x-cosx\)

Answer 28

a) y=x3−3x2+2020xy=x3−3x2+2020x.

+ Ta có tập xác định: D=RD=R.

+ y′=(x3−3x2+2020x)′y′=(x3−3x2+2020x)′=(x3)′−(3x2)′+(2020x)′=(x3)′−(3x2)′+(2020x)′=3x2−6x+2020=3x2−6x+2020
y′=3b) y=cos3x−sinxy=cos⁡3x−sin⁡x.

+ Ta có tập xác định: D=RD=R.

+ y′=(cos3x−sinx)′y′=(cos⁡3x−sin⁡x)′=(cos3x)′−(sinx)′=(cos⁡3x)′−(sin⁡x)′=−(3x)′sin3x−cosx=−(3x)′sin⁡3x−cos⁡x=−3sin3x−cosx=−3sin⁡3x−cos⁡x.

 

Answer 29

  

Answer 30