Chọn B.
Giả sử w = x + yi (x, y ∈ R) là một căn bậc hai của số phức z = 8 + 6i.
![]()
![]()
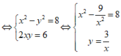
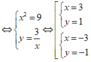
Do đó z có hai căn bậc hai là 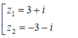
Chọn B.
Giả sử w = x + yi (x, y ∈ R) là một căn bậc hai của số phức z = 8 + 6i.
![]()
![]()
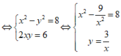
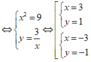
Do đó z có hai căn bậc hai là 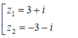
Biết số phức z thỏa mãn đồng thời hai điều kiện z - 3 - 4 i = 5 và biểu thức M = | z + 2 | 2 - | z - i | 2 đạt giá tri lớn nhất. Tính môđun của số phức z+i
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn phương trình 4|z+i| + 3|z-i| = 10. Tính giá trị nhỏ nhất của |z|
A. 1 2
B. 5 7
C. 3 2
D. 1
Cho hai số phức z = (2x+3) + (3y-1)i và z' = (y-1)i. Ta có z = z' khi:
A . x = 3 2 ; y = 0
B . x = - 3 2 ; y = 0
C . x = 3 ; y = 1 3
D . x = 0 ; y = - 3 2
Cho số phức thỏa mãn: z=a+bi, ( a , b ∈ R ) thỏa mãn: z ( 2 + i ) = z - 1 + i ( 2 z + 3 ) . Tính S = a + b
![]()
![]()
![]()
![]()
Trong mặt phẳng Oxy, gọi A là điểm biểu diễn số phức z thỏa mãn:\(\left(1-2i\right)z-\dfrac{2-i}{1+i}=\left(3-i\right)z\) . Tọa độ trung điểm I của OA là
A: I \(\left(\dfrac{1}{20};\dfrac{7}{20}\right)\)
B: I \(\left(\dfrac{1}{5};\dfrac{7}{5}\right)\)
C:I \(\left(\dfrac{1}{10};\dfrac{7}{10}\right)\)
D:I \(\left(\dfrac{1}{16};\dfrac{7}{16}\right)\)
Cho số phức z thỏa mãn z + ( 2 + i ) z ¯ = 3 + 5 i . Tính môđun của số phức z.
![]()
![]()
![]()
![]()
Cho hai số phức z=(2x+3) + (3y-1)i và z'=3x + (y+1)i. Khi z=z', chọn khẳng định đúng.
![]()
![]()
![]()
![]()
Có bao nhiêu số phức z thỏa mãn z ( z - 3 - i ) + 2 i = ( 4 - i ) z ?
![]()
![]()
![]()
![]()
Cho số phức z=a+bi với a,b thuộc R thỏa mãn z-3+i=|z|i . Giá trị của a+b bằng
A. -1
B.7.
C.5.
D.12.
Số phức z thỏa mãn 3 - 2 i + z ¯ i là số thực và z + i = 2 ,Phần ảo của z là:
![]()
![]()
![]()
![]()