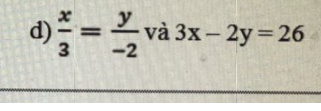Question

Tìm x,y

Nhanh nhé

Answer 1

Áp dụng tc dtsbn:

\(\dfrac{x}{3}=\dfrac{y}{-2}=\dfrac{3x-2y}{3\cdot3-2\left(-2\right)}=\dfrac{26}{13}=2\\ \Leftrightarrow\left\{{}\begin{matrix}x=6\\y=-4\end{matrix}\right.\)

Answer 2

Giải thích các bước giải:

 \(\dfrac{x}{3}=\dfrac{y}{-2}\)

Áp dụng t/c dãy tỉ số bằng nhau ta có:

\(\dfrac{3x}{9}=\dfrac{2x}{-4}=\dfrac{3x-2x}{9-\left(-4\right)}=\dfrac{26}{13}=2\)

\(=>\dfrac{y}{-2}=2=>y=-4\)

Vậy