\(-TH1:\left|4-x\right|=4-x\\ =>\left(4-x\right):3=\left|-\dfrac{6}{5}\right|\\ =>\left(4-x\right):3=\dfrac{6}{5}\\ =>4-x=\dfrac{6}{5}\times3\\ =>4-x=\dfrac{18}{5}\\ =>x=4-\dfrac{18}{5}\\ =>x=\dfrac{2}{5}\\ -TH2:\left|4-x\right|=x-4\\ =>\left(x-4\right):3=\left|-\dfrac{6}{5}\right|\\ =>\left(x-4\right):3=\dfrac{6}{5}\\ =>x-4=\dfrac{6}{5}\times3\\ =>x-4=\dfrac{18}{5}\\ =>x=\dfrac{18}{5}+4\\ =>x=\dfrac{38}{5}\)
Vậy \(S=\left\{\dfrac{38}{5};\dfrac{2}{5}\right\}\)


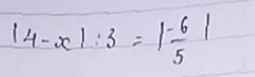












 b./
b./  c*./
c*./ 
 b/
b/  =
=  e/
e/  =
=  và
và  e) 9x =81
e) 9x =81 
 h)
h)  và x + y= -21 i)
và x + y= -21 i)  và 3x - 2y = -2
và 3x - 2y = -2 và 3x – 2y – z = -29
và 3x – 2y – z = -29