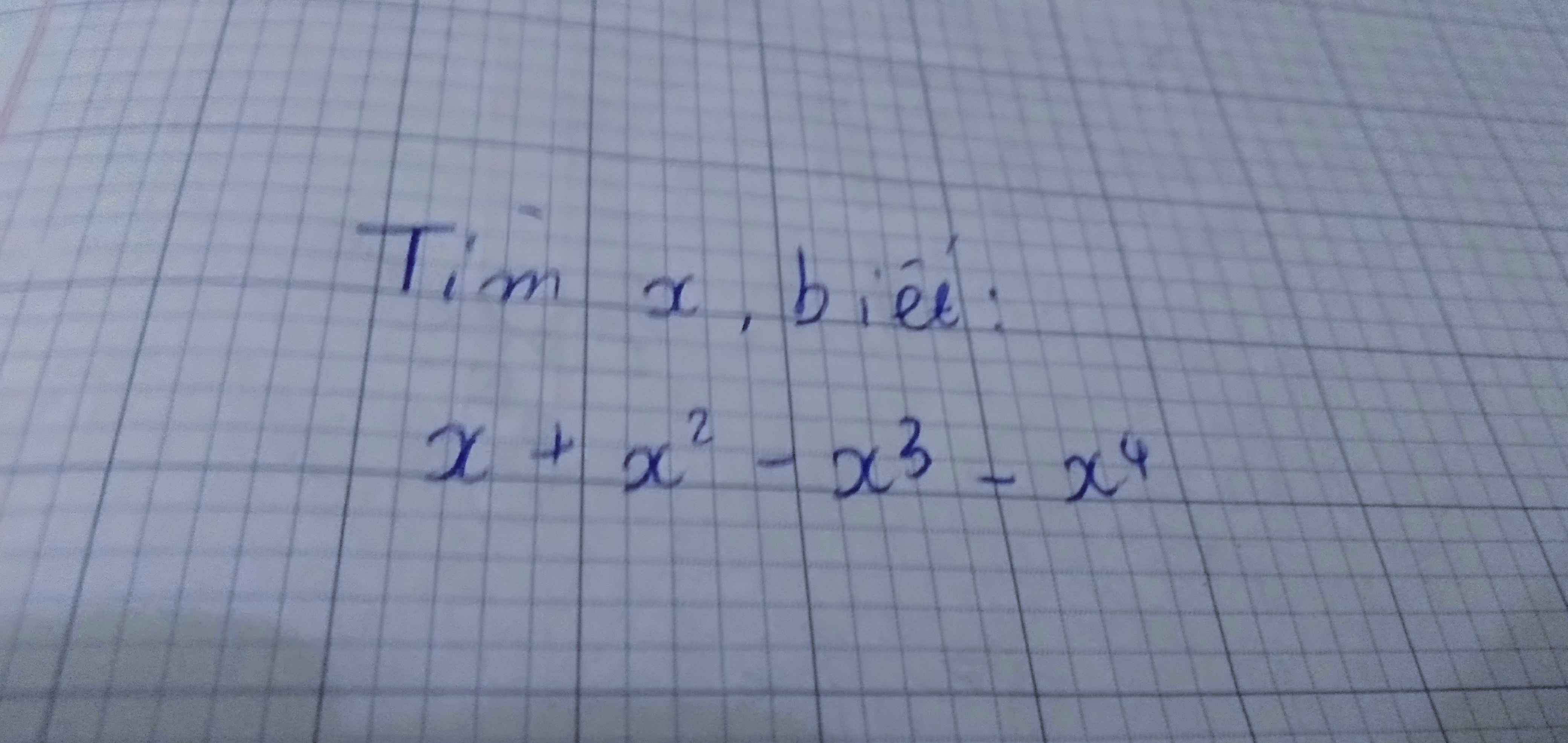`x+x^2-x^3-x^4=0`
`<=>x(1+x-x^2-x^3)=0`
`<=>x[(x+1)-x^2(x+1)]=0`
`<=>x(x+1)(1-x^2)=0`
`<=>x(x+1)(1+x)(1-x)=0`
`<=>x(x+1)^2(1-x)=0`
`<=>` \(\left[ \begin{array}{l}x=0\\(x+1)^2=0\\1-x=0\end{array} \right.\)
`<=>` \(\left[ \begin{array}{l}x=0\\x=-1\\x=1\end{array} \right.\)
Vậy `S={0,1,-1}`
\(x+x^2-x^3-x^4=x\left(x+1\right)-x^3\left(x+1\right)\)
\(=\left(x-x^3\right)\left(x+1\right)\)
\(=x\left(1-x^2\right)\left(x+1\right)\)