Các câu hỏi tương tự
Cho hàm số y x3 + x – 2 có đồ thị (C). Tìm tọa độ giao điểm của (C) và trục tung A. (0;-2). B. (1;0). C. (-2;0). D. (0;1).
Đọc tiếp
Cho hàm số y = x3 + x – 2 có đồ thị (C). Tìm tọa độ giao điểm của (C) và trục tung
A. (0;-2).
B. (1;0).
C. (-2;0).
D. (0;1).
Cho hàm số y f(x)
a
x
+
b
c
x
+
d
( a,b,c,d
∈
ℝ
,
-
d
c
≠
0) đồ thị hàm số y f’(x) như hình vẽ. Biết đồ thị hàm số y f(x) cắt...
Đọc tiếp
Cho hàm số y = f(x) = a x + b c x + d ( a,b,c,d ∈ ℝ , - d c ≠ 0) đồ thị hàm số y= f’(x) như hình vẽ.

Biết đồ thị hàm số y= f(x) cắt trục tung tại điểm có tung độ bằng 3. Tìm phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành ?
A. y = x - 3 x + 1
B. y = x + 3 x - 1
C. y = x + 3 x + 1
D. y = x - 3 x - 1
Tọa độ giao điểm của đồ thị các hàm số:
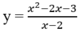
và y = x + 1 là:
A. (2; 2); B. (2; -3);
C(-1; 0); D. (3; 1).
Cho hàm số
y
x
+
2
2
x
+
3
có đồ thị (C). Giả sử, đường thẳng d: ykx+m là tiếp tuyến của (C), biết rằng d cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác
∆
O
A
B
cân tại gốc tọa độ O. Tổng k+m có giá trị bằng: A. 1. B. 3. C. -1. D. -3.
Đọc tiếp
Cho hàm số y = x + 2 2 x + 3 có đồ thị (C). Giả sử, đường thẳng d: y=kx+m là tiếp tuyến của (C), biết rằng d cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác ∆ O A B cân tại gốc tọa độ O. Tổng k+m có giá trị bằng:
A. 1.
B. 3.
C. -1.
D. -3.
Cho hàm số y x4-2( m+1)x2+ m ( C). Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số C có ba điểm cực trị A: B; C sao cho OA BC ; trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung, B và C là hai điểm cực trị còn lại. A.
m
2
±
2
2
B.
m
2
+
2
2
C.
m
2...
Đọc tiếp
Cho hàm số y= x4-2( m+1)x2+ m ( C). Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số C có ba điểm cực trị A: B; C sao cho OA= BC ; trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung, B và C là hai điểm cực trị còn lại.
A. m = 2 ± 2 2
B. m = 2 + 2 2
C. m = 2 - 2 2
D. m = ± 1
Cho hàm số
y
x
4
-
2
(
m
+
1
)
x
2
+
m
(
C
)
. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số (C) có b...
Đọc tiếp
Cho hàm số y = x 4 - 2 ( m + 1 ) x 2 + m ( C ) . Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số (C) có ba điểm cực trị A, B, C sao cho OA = BC; trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung, B và C là hai điểm cực trị còn lại
A. m = 2 ± 2 2
B. m = 2 + 2 2
C. m = 2 - 2 2
D. m = ± 1
Biết hàm số yf(x) có
f
(
x
)
3
x
2
+
2
x
-
m
+
1
,
f
(
2
)
1
và đồ thị của hàm số yf(x) cắt trục tung tại điểm có tung độ bằng -5. Hàm số f(x) là:
Đọc tiếp
Biết hàm số y=f(x) có f ' ( x ) = 3 x 2 + 2 x - m + 1 , f ( 2 ) = 1 và đồ thị của hàm số y=f(x) cắt trục tung tại điểm có tung độ bằng -5. Hàm số f(x) là:
![]()
![]()
![]()
![]()
Biết hàm số yf(x) có
f
(
x
)
3
x
2
+
2
x
-
m
+
1
, f(2)1 và đồ thị của hàm số yf(x) cắt trục tung tại điểm có tung độ bằng –5. Hàm số f(x) là
Đọc tiếp
Biết hàm số y=f(x) có f ' ( x ) = 3 x 2 + 2 x - m + 1 , f(2)=1 và đồ thị của hàm số y=f(x) cắt trục tung tại điểm có tung độ bằng –5. Hàm số f(x) là
![]()
![]()
![]()
![]()
Tọa độ giao điểm của đồ thị các hàm số:
y
x
2
-
2
x
-
3
x
-
2
và y x + 1 là:A. (2; 2); B. (2; -3);C(-1; 0); D....
Đọc tiếp
Tọa độ giao điểm của đồ thị các hàm số: y = x 2 - 2 x - 3 x - 2
và y = x + 1 là:
A. (2; 2); B. (2; -3);
C(-1; 0); D. (3; 1).



