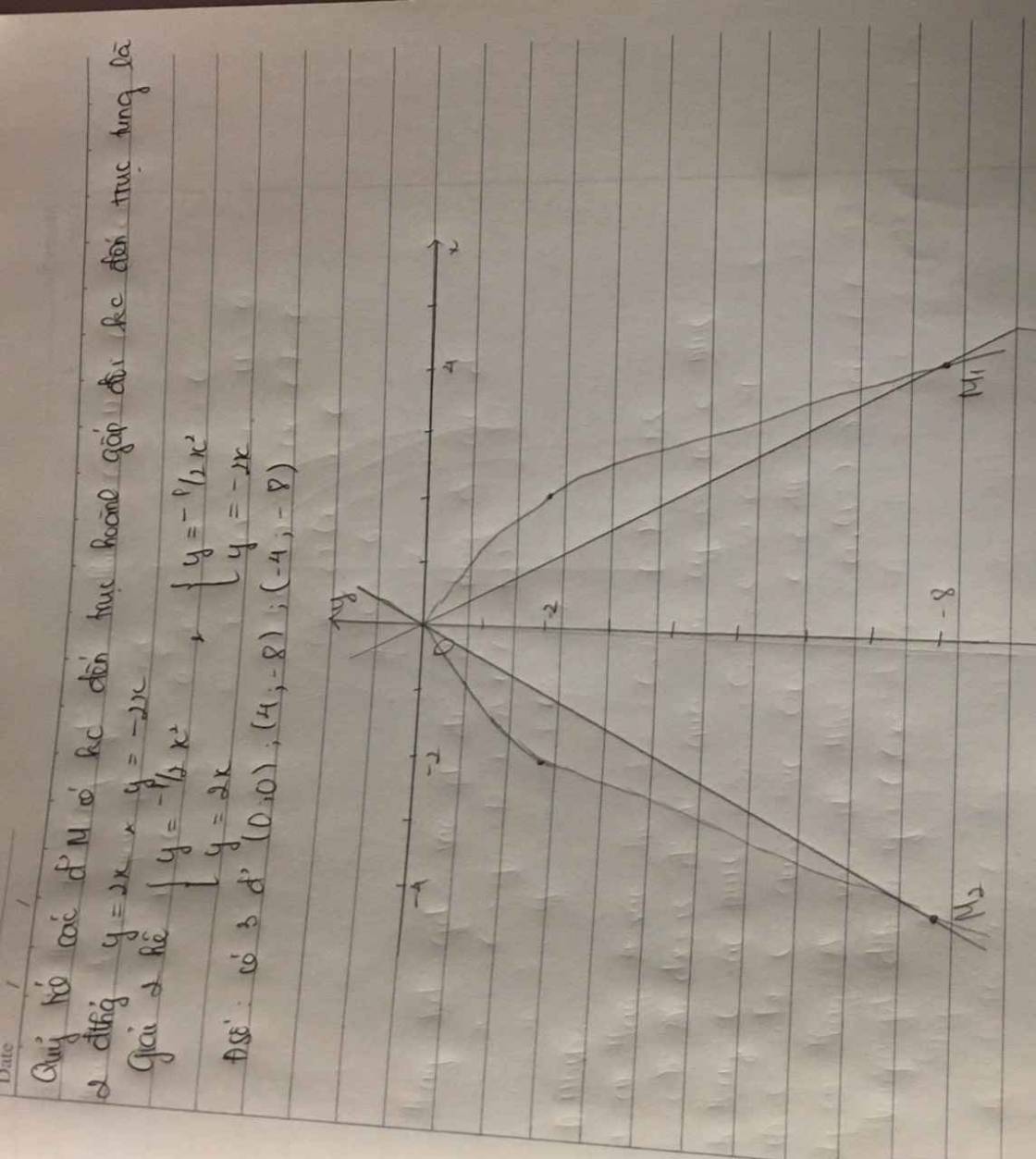
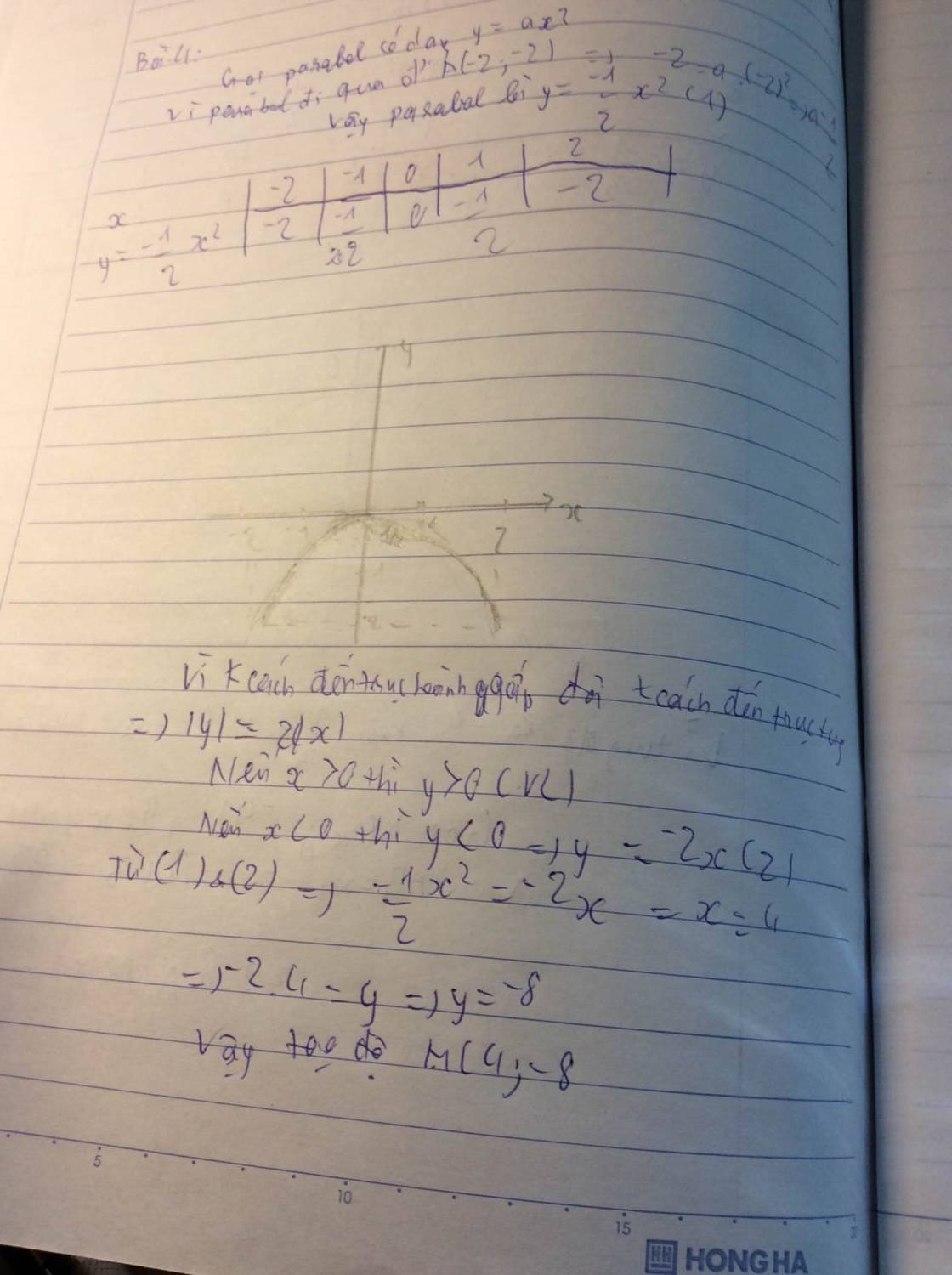
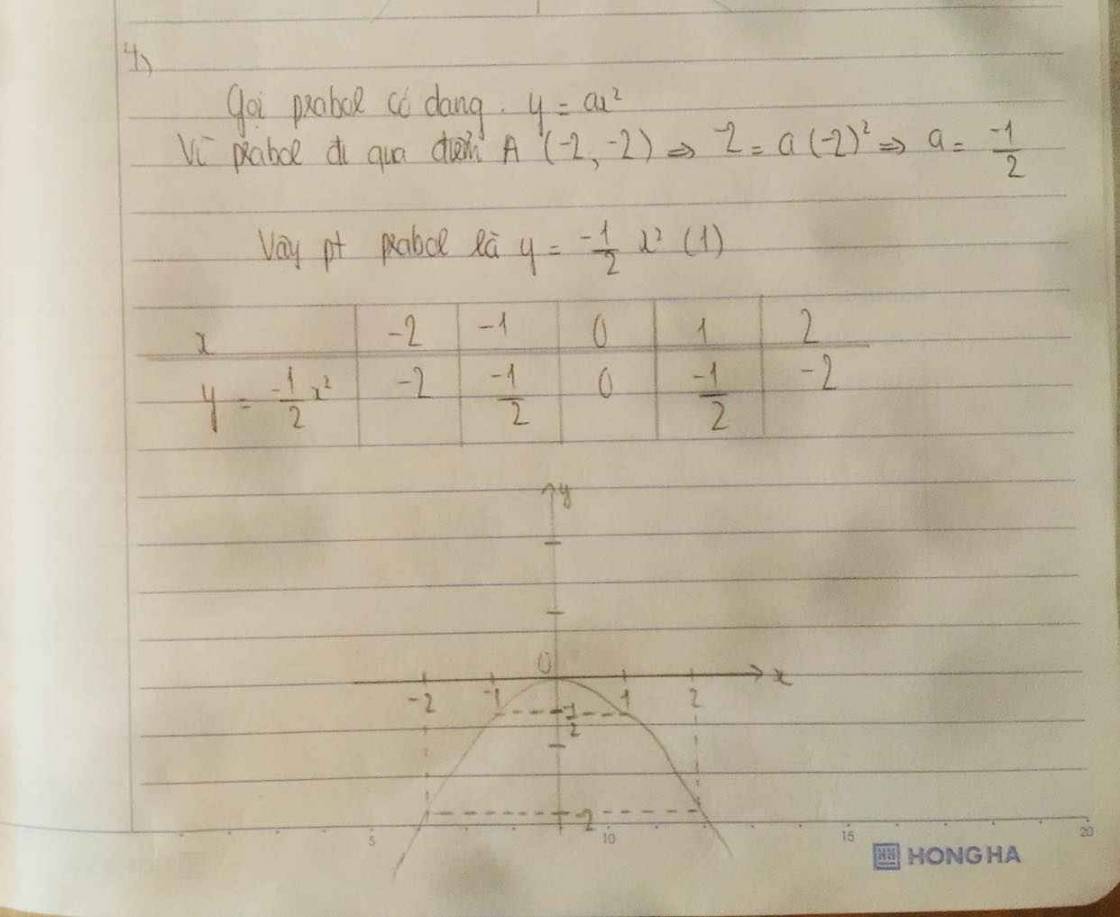
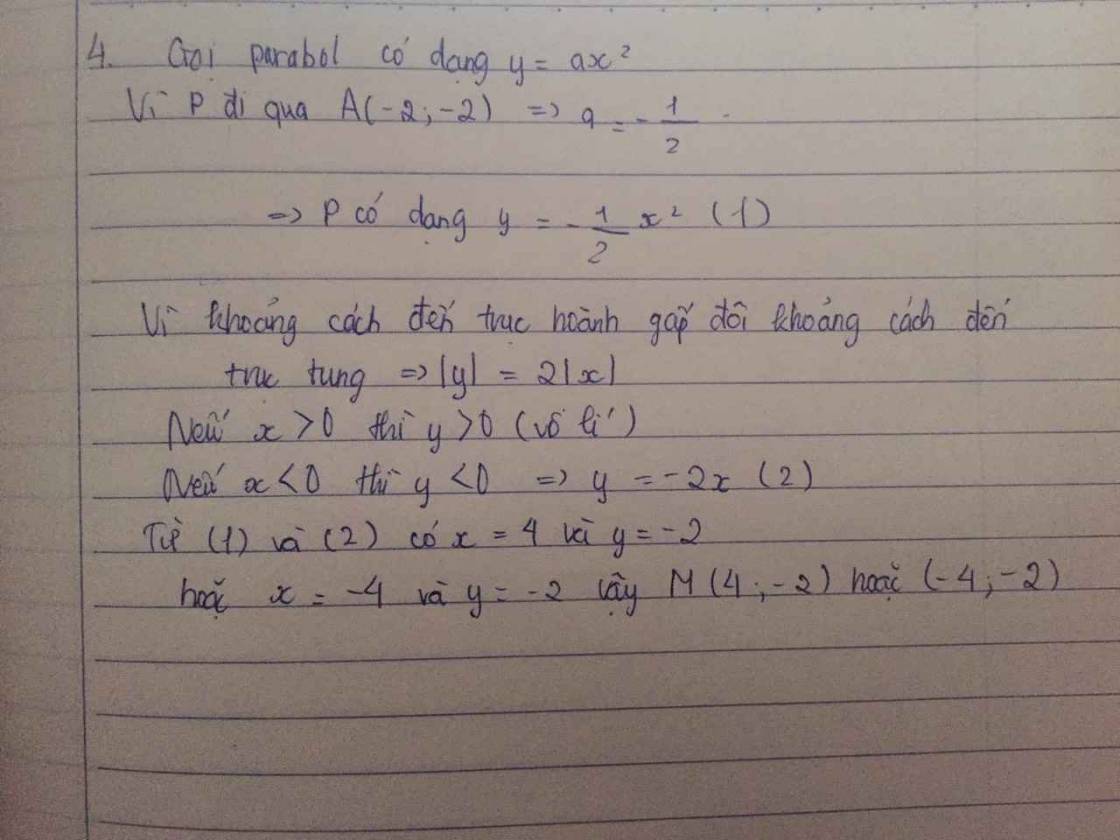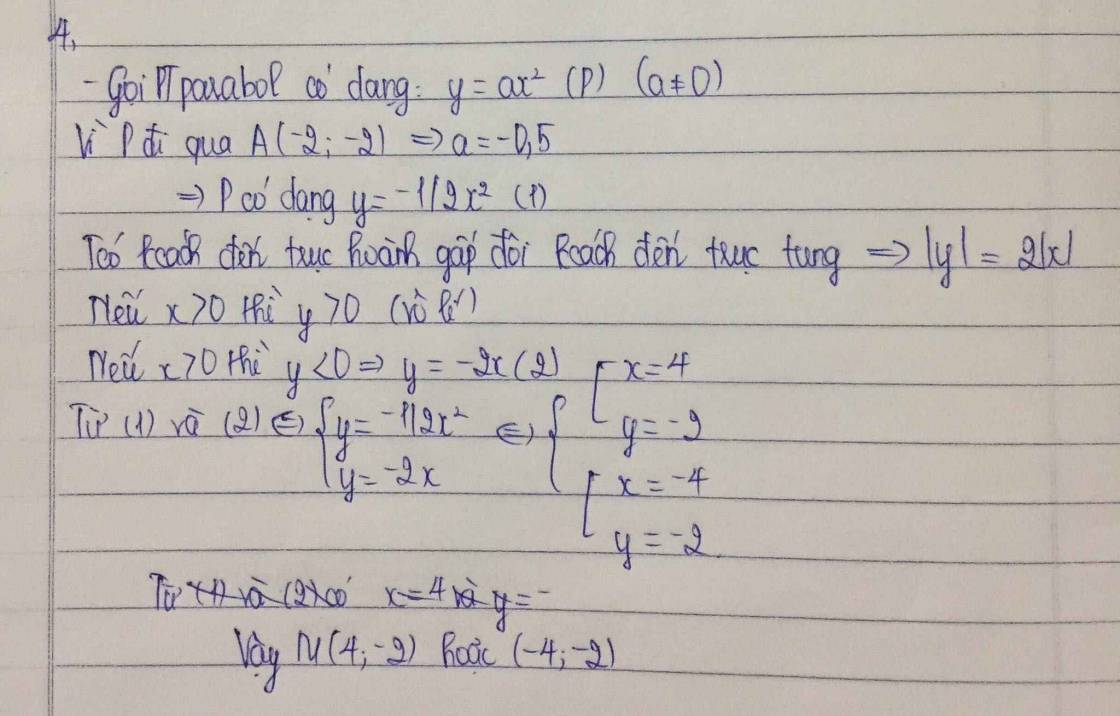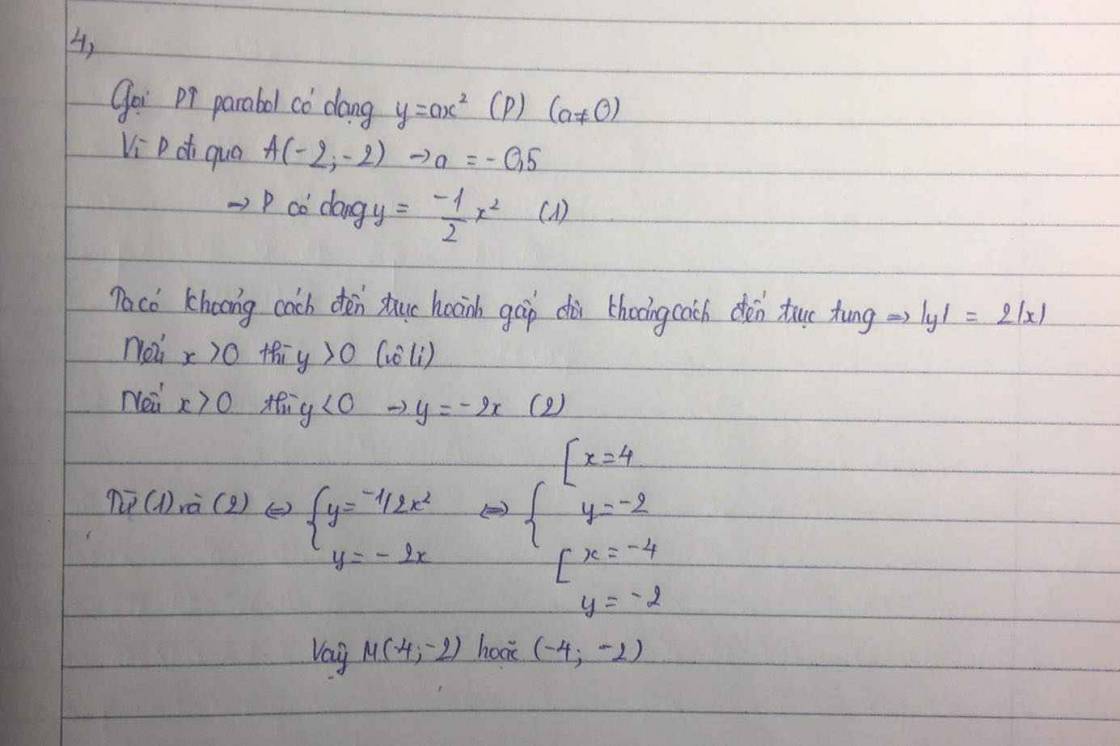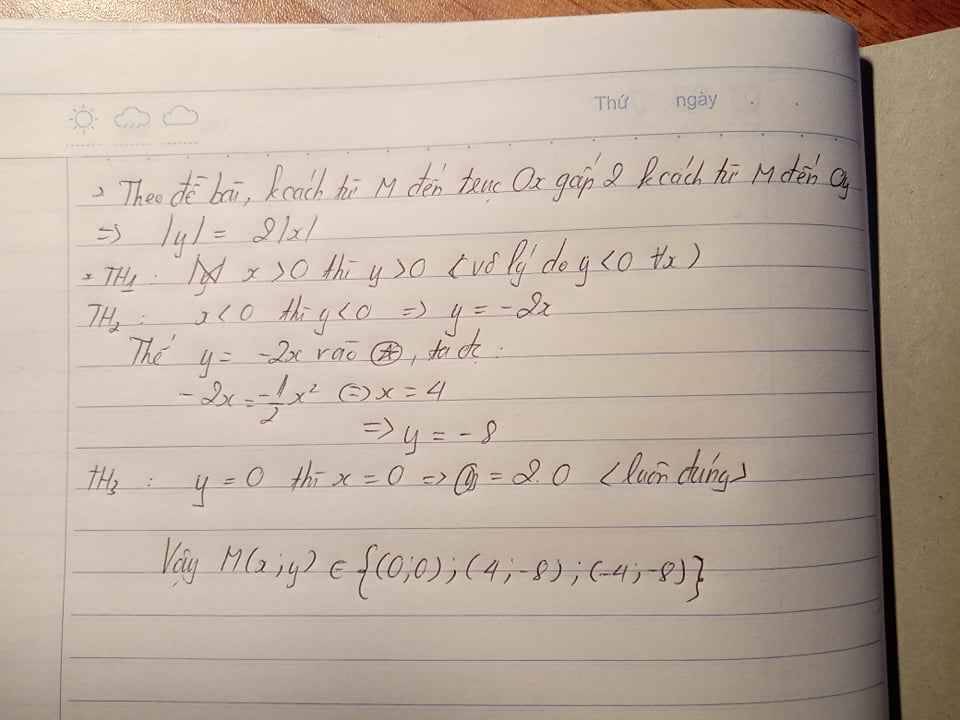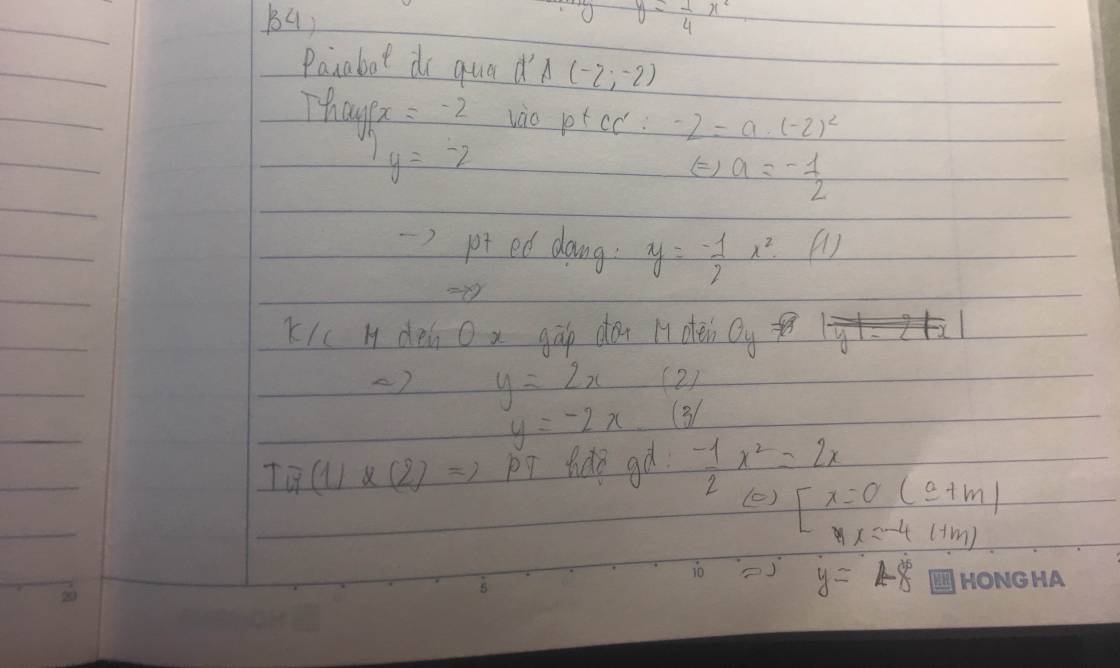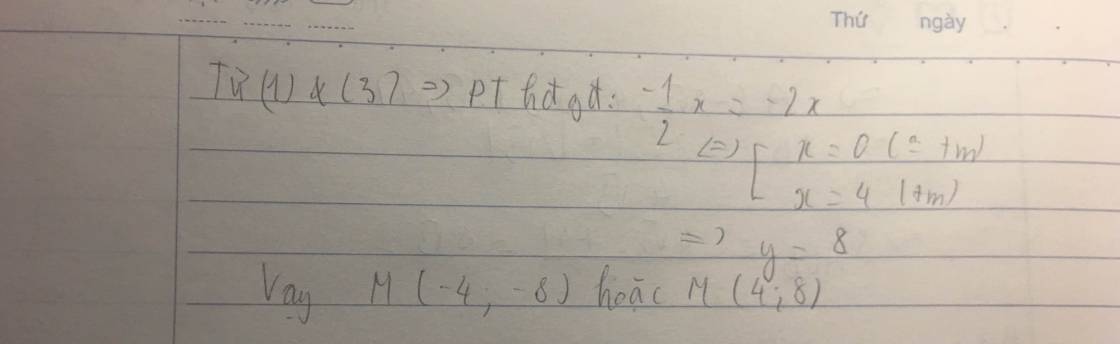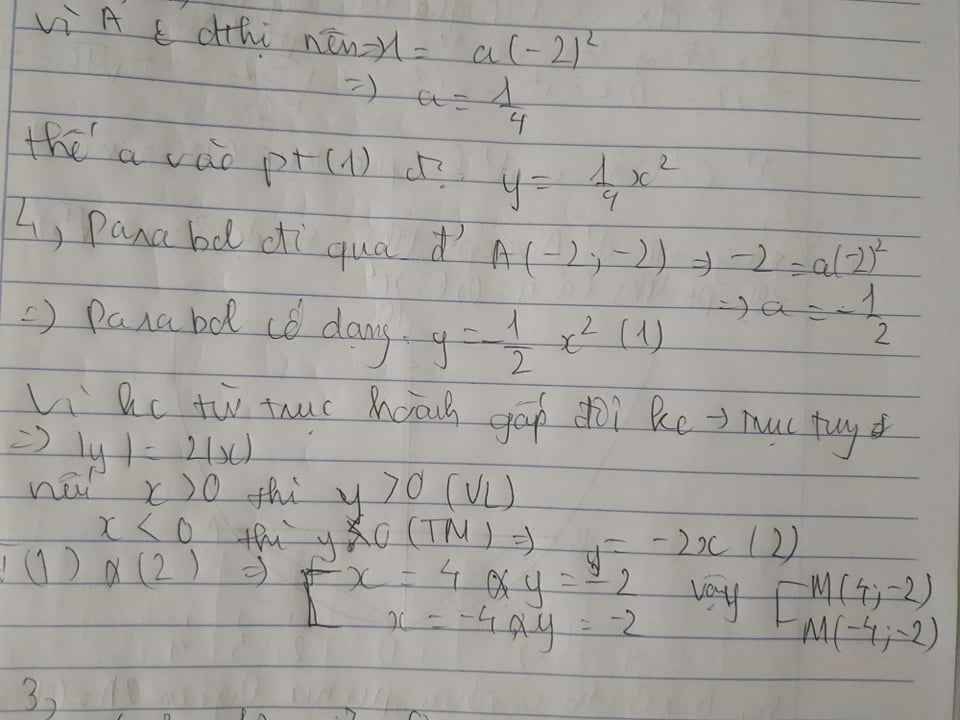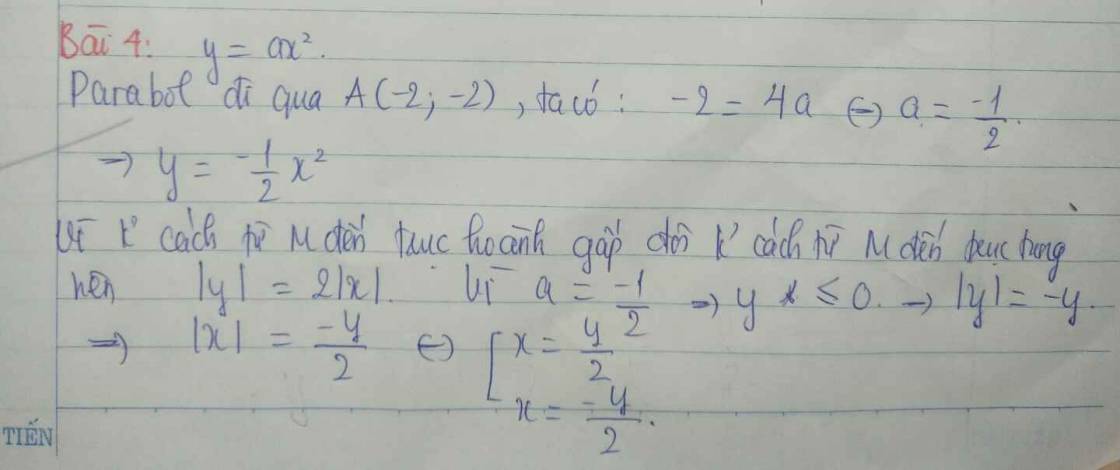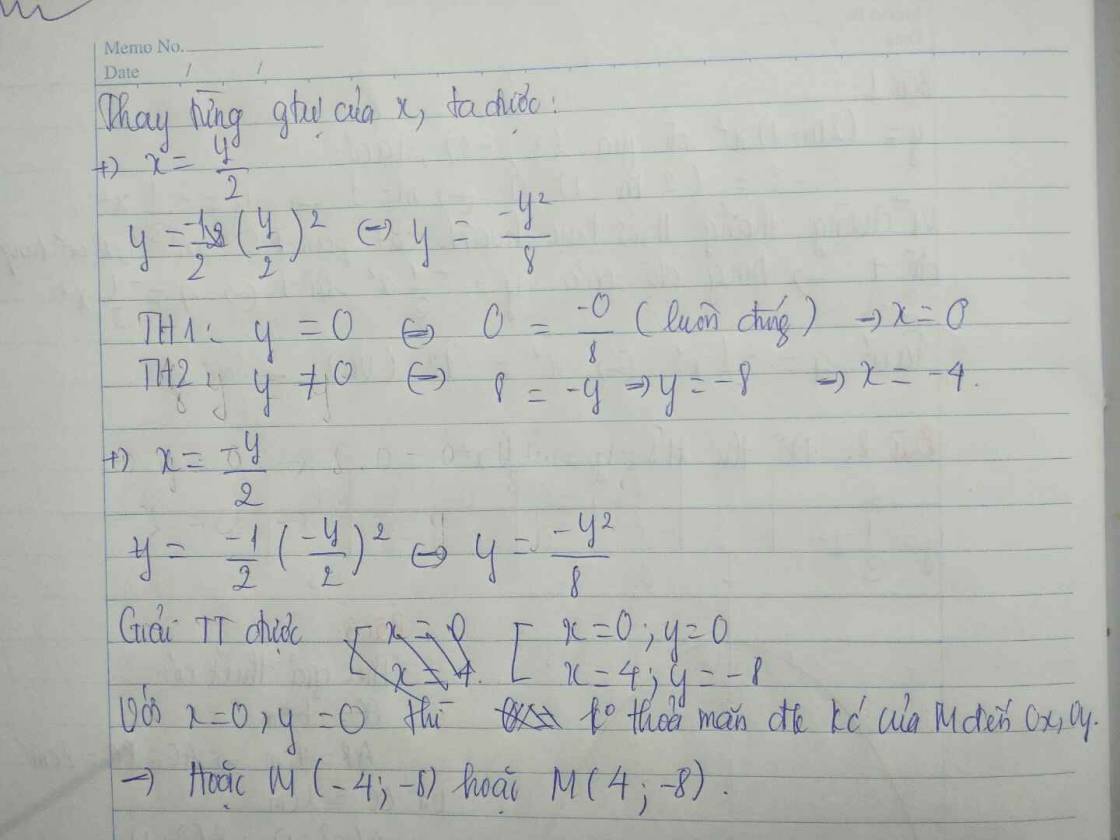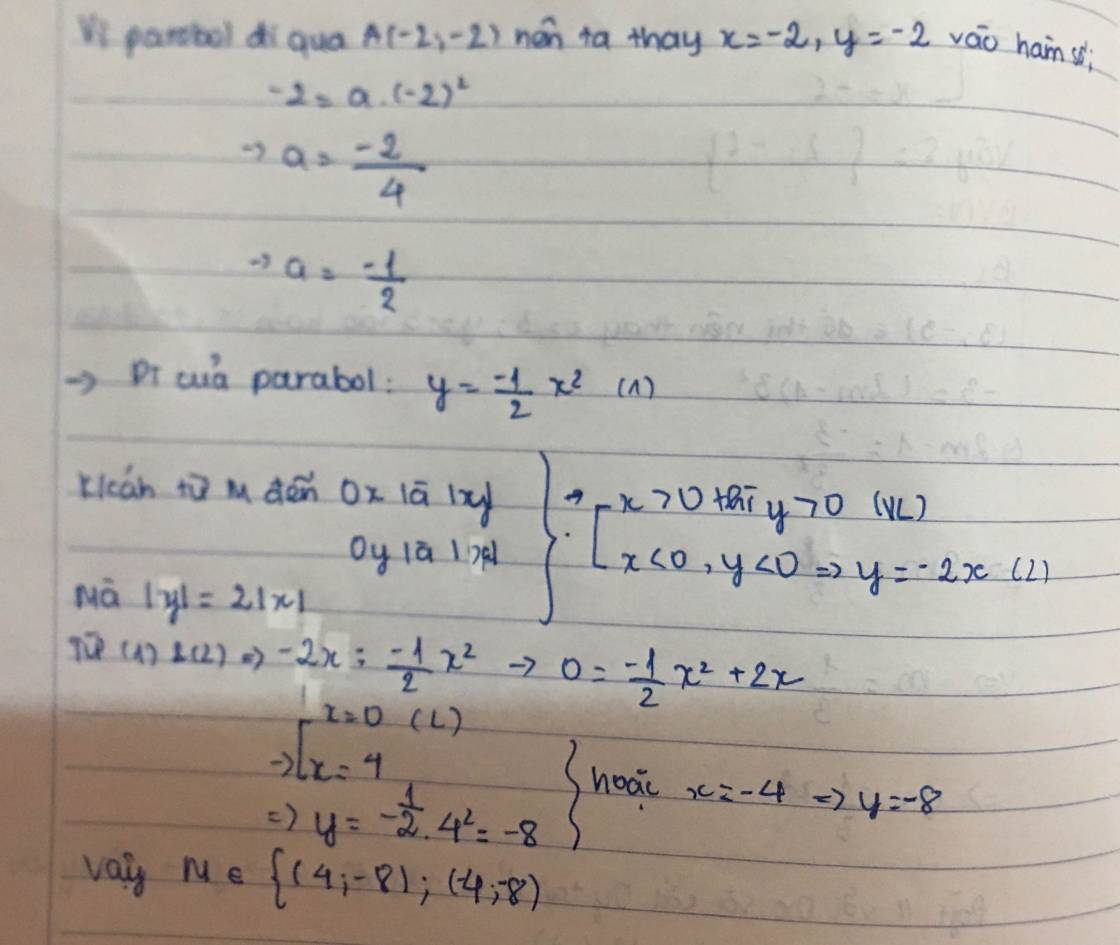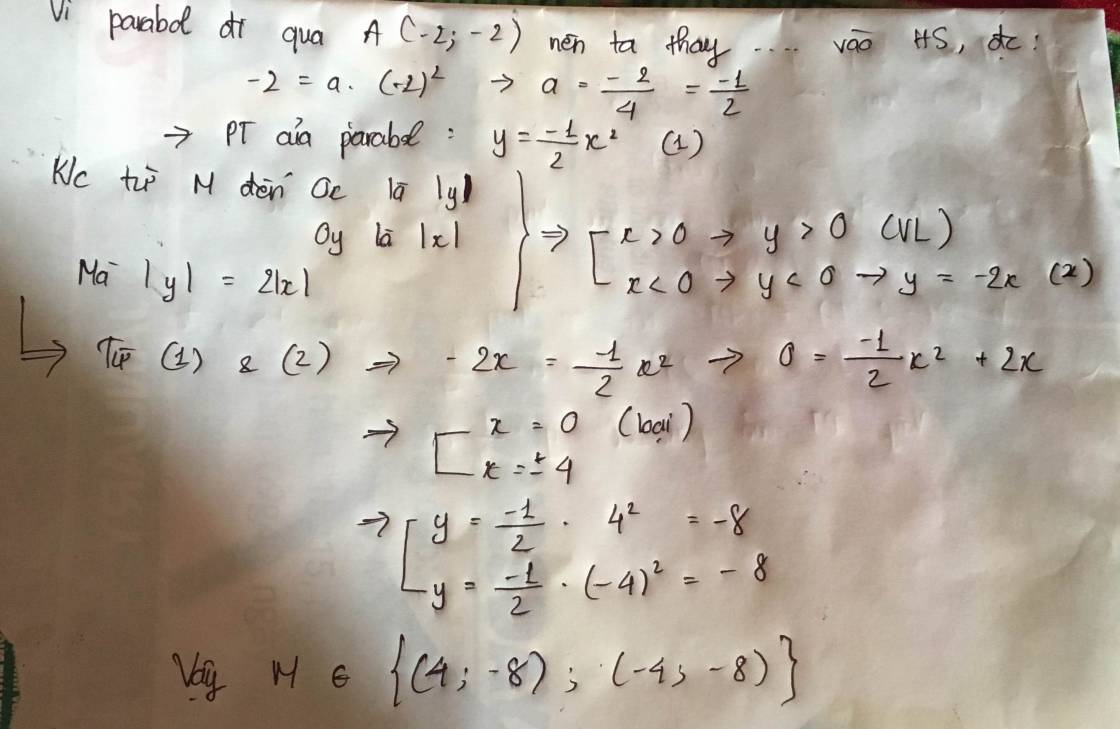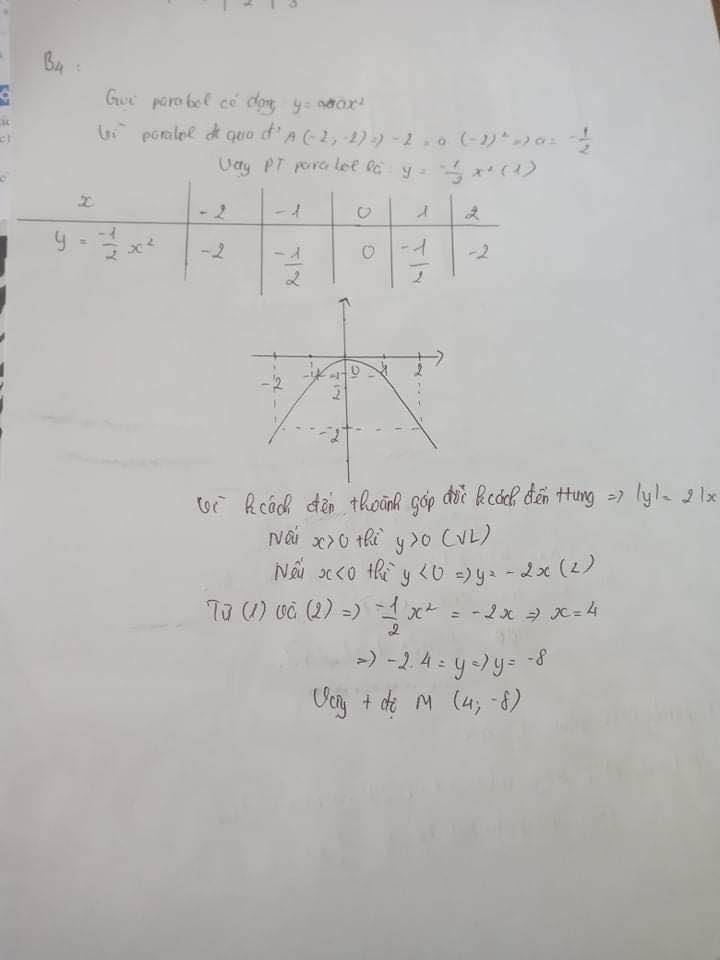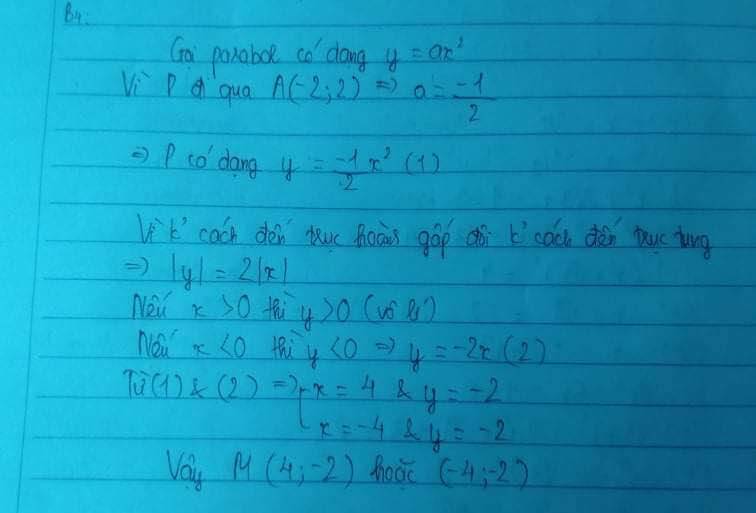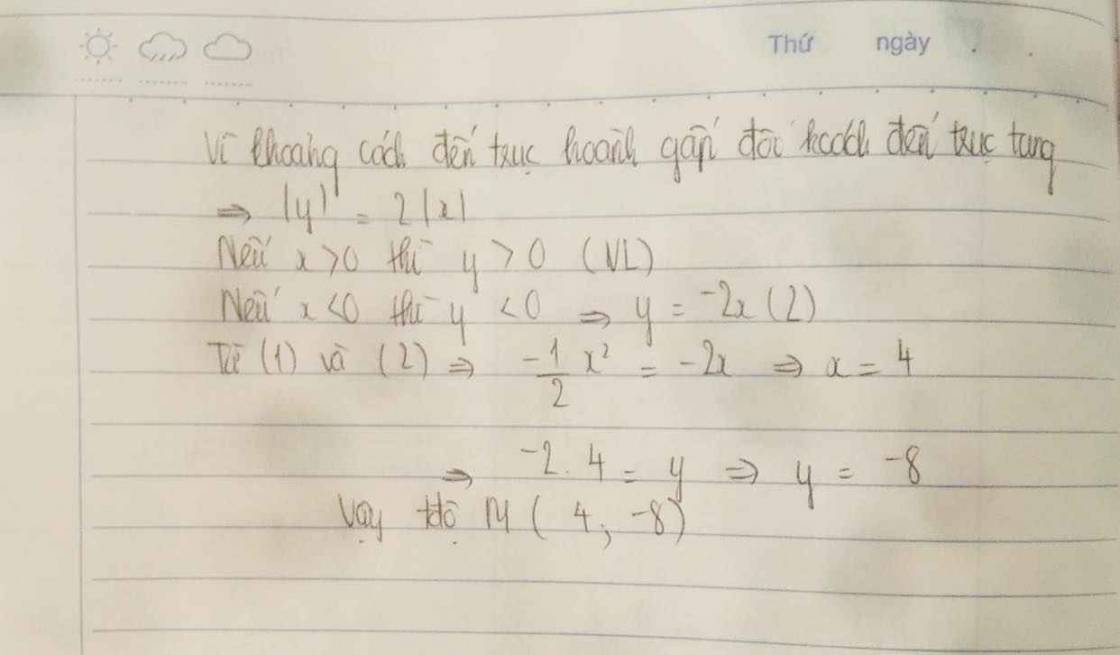Gọi parabol có dạng y=ax2
Vì P đi qua A(-2;-2)\(\Rightarrow\)a=-\(\dfrac{1}{2}\)
\(\Rightarrow\)P có dạng y= -\(\dfrac{1}{2}\)x2 (1)
vì khoảng cách đến trục hoành gấp đôi khoảng cách đến trục tung\(\Rightarrow\)\(\left|y\right|\)=2\(\left|x\right|\)
Nếu x>0 thì y>0 (vô lí)
Nếu x<0 thì y<0\(\Rightarrow\)y=-2x (2)
Từ (1) và (2) có x=4 và y=-2
hoặc x=-4 và y= -2
vậy M(4;-2) hoặc(-4;-2)
Parabol y=ax\(^2\) đi qua điểm A (-2;-2)
⇒-2=a.(-2)\(^2\)
⇒a=-\(\dfrac{1}{2}\)
⇒y=-\(\dfrac{1}{2}\).x\(^2\)
M(4;-2) hoặc M(-4;-2)
Khoảng cách điểm M(x ; y) đến trục tung (Oy) là |x|, đến trục hoành (Ox) là |y|.
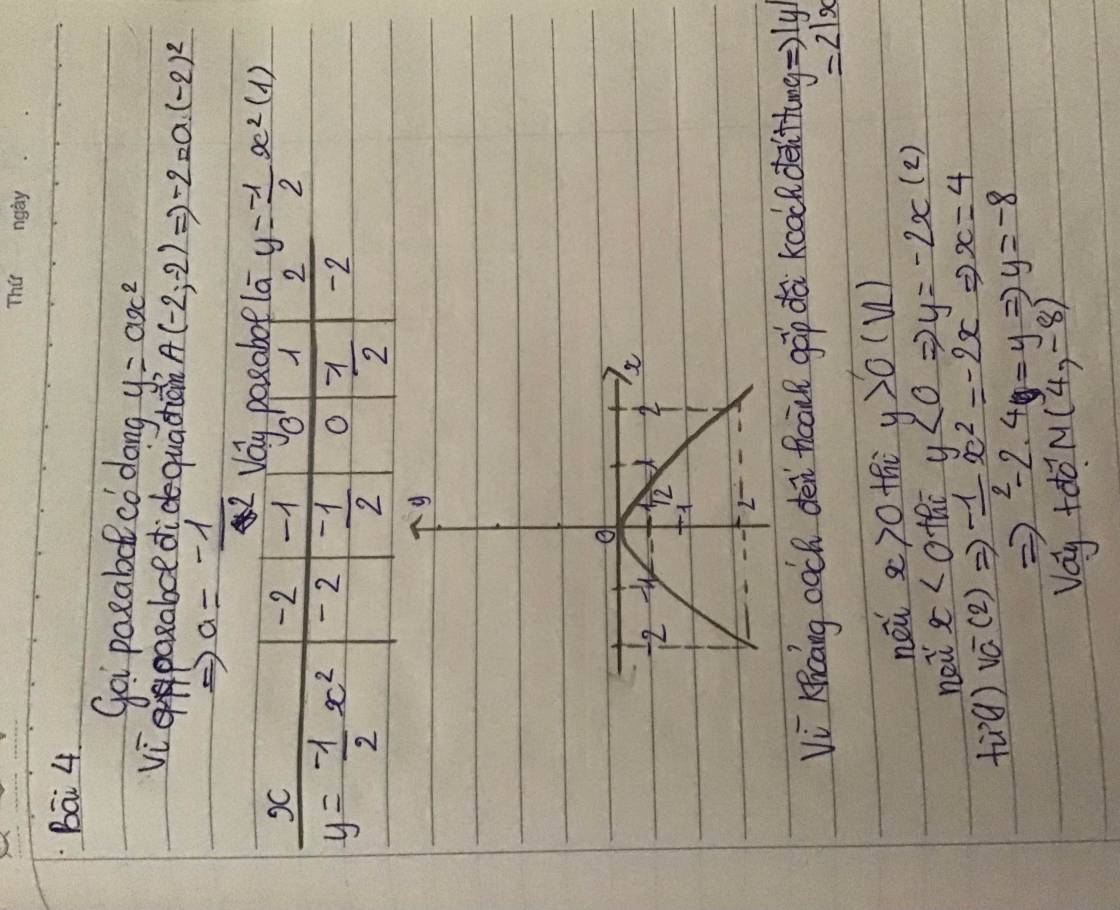
parabol đi qua điểm A(-2 ; -2) ⇒ -2=a.(-2)2 ⇒ a=-\(\dfrac{1}{2}\)
⇒parabol có dạng y=-\(\dfrac{1}{2}\)x2
khoảng cách từ M đến trục hoành gấp đôi khoảng cách từ M đến trục tung ⇒ |y|=2|x|
nếu x>0 ⇒ y>0(vô lí)
Nếu x<0 ⇒ y<0 (luôn đúng) ⇒ y=-2x
M ϵ parabol ⇒ Ta có pt hoàng độ giao điểm: -\(\dfrac{1}{2}\)x2=-2x
⇒-\(\dfrac{1}{2}\)x2+2x=0 ⇔ x=4 ⇒ y = 8
Vậy toạ độ M (4;8)