Đáp án A
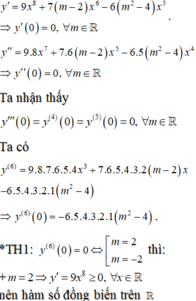

Vậy có 3 giá trị nguyên của tham số m
Đáp án A
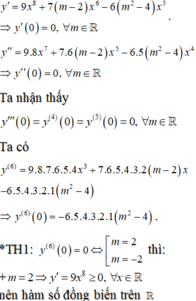

Vậy có 3 giá trị nguyên của tham số m
Câu 9 tìm tất cả tham số thực m để hàm số\(y=\left(m-1\right)x^4-\left(m^2-2\right)x^2+2019\) đạt cực tiểu tại x=-1
Bài 1. Cho hàm số: y = 1/3 x3 - mx2 +(m2 - m + 1)x + 1. Với giá trị nào của m thì hàm số đạt cực đại tại điểm x = 1
Bài 2. Cho hàm số y = 1/3 x3 + (m2 - m + 2) x2 + (3m2 + 1)x + m - 5. Tìm m để hàm số đạt cực tiểu tại x = -2 .
Bài 3. Cho hàm số y = 1/3 x3 - (m+1) x2 + (m2 + 2m)x + 1 (m là tham số). Tìm tất cả tham số thực m để hàm số đạt cực tiểu tại x = 2.
Bài 4. Tìm tất cả tham số thực m để hàm số y = (m-1)x4 - (m2 - 2) x2 + 2016 đạt cực tiểu tại
x = -1.
Bài 5. Tìm giá trị của tham số m để hàm số y = x3/3 +(2m - 1)x2 + (m - 9)x + 1 đạt cực tiểu tại
x = 2 .
Đừng hỏi tại sao tui ngu!!!
Giúp.com.vn
Tìm tất cả các giá trị thực của tham số m để hàm số y = 1 3 x 3 + ( m 2 - m + 2 ) x 2 + ( 3 m 2 + 1 ) x đạt cực tiểu tại x = - 2
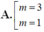
B. m = 3 .
C. . m = 1
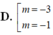
Câu 3 Để đồ thị hàm số \(y=-x^4-\left(m-3\right)x^2+m+1\) có điểm cực đạt mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là
Câu 4 Cho hàm số \(y=x^4-2mx^2+m\) .Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị
Cho hàm số y = m 3 x 3 + ( m - 2 ) x 2 + ( m - 1 ) x + 2 , với m là tham số thực. Tìm tất cả các giá trị thực của tham số m sao cho hàm số đạt cực đại tại điểm x 1 và đạt cực tiểu tại điểm x 2 thỏa mãn x 1 < x 2
A. 0 < m < 4 3
B. m ≤ 0
C. 5 4 < m < 4 3
D. Không tồn tại m thỏa mãn
Câu 1: Tìm giá trị thực của tham số m để hàm số
y= \(\dfrac{1}{3}x^3-mx^{2^{ }}+\left(m^2-4\right)x+3\) tại x=3
Câu 2:Tìm m để hàm số \(y=x^3-2mx^2+mx+1\) đạt cực tiểu tại x=1
Tìm tất cả các giá trị thực của tham số m để hàm số y = 1 3 x 3 - m x 2 + ( m + 1 ) x - 1 đạt cực đại tại x = - 2 ?
A. Không tồn tại m
B. -1
C. 2
D. 3
Câu 3: Tìm tất cả các giá trị của tham số m để hàm số \(y=x^3-3x^2+mx+1\) đạt cực tiểu tại x=2