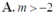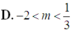Question

Tìm tất cả các giá trị thực của tham số m để bất phương trình 2^3x + (m – 1)3^x + m – 1 > 0 nghiệm đúng với mọi  x ∈ ℝ .

A.  m ∈ ℝ

B.  m > 1

C.  m ≤ 1

D.  m ≥ 1

Answer 1

Đáp án D

BPT <=> 2^3x + (m – 1)3^x + m – 1 > 0

<=> 2^3x – 3^x  – 1 + m(3^x + 1) > 0

⇔ m > 3 x - 8 x + 1 3 x + 1 ; ∀ x ∈ ℝ (*).

Xét hàm số  f x = 3 x - 8 x + 1 3 x + 1 ; ∀ x ∈ ℝ , ta có

f ' x = 8 x ln   3 - ln   8 . 3 x - ln   8 3 x + 1 2 < 0 ; ∀ x ∈ ℝ .

Suy ra f(x) là hàm số nghịch biến trên  ℝ .

Mà  lim x → - ∞ f x = 1 , do đó

m i n x ∈ ℝ f x = lim x → - ∞ f x = 1 .

Vậy (*)  ⇔ m ≥ m i n x ∈ ℝ f x = 1 ⇒ m ≥ 1  là giá trị cần tìm.