Các câu hỏi tương tự
Biết S = (a,b) là tập hợp tất cả các giá trị của tham số m để đường thẳng y = m cắt đồ thị hàm số y = | \(x^2-4x+3\) | tại bốn điểm phân biệt . Tìm a + b
Cho hai đường thẳng d: (m – 2)x +(m – 6)y + m – 1 0, ∆: (m – 4)x + (2m – 3)y – m + 5 0. Tất cả giá trị của m để hai đường thẳng cắt nhau là A.m ≠ 3 B.m ≠ 6 C.m ≠ 3 và m ≠ - 6 D.không có m thỏa mãn
Đọc tiếp
Cho hai đường thẳng d: (m – 2)x +(m – 6)y + m – 1= 0, ∆: (m – 4)x + (2m – 3)y – m + 5 = 0. Tất cả giá trị của m để hai đường thẳng cắt nhau là
A.m ≠ 3
B.m ≠ 6
C.m ≠ 3 và m ≠ - 6
D.không có m thỏa mãn
Tìm tất cả các giá trị thực của tham số m để đường thẳng (d): y (3m + 2)x -7m – 1 vuông góc với đường thẳng
(
∆
)
:
y
2
x
-
1
A. m 0. B. C. D.
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đường thẳng (d): y = (3m + 2)x -7m – 1 vuông góc với đường thẳng ( ∆ ) : y = 2 x - 1
A. m = 0.
B. ![]()
C. ![]()
D. 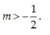
Tìm tất cả các giá trị thực của tham số m để đường thẳng d: y = (3m + 2)x − 7m − 1 vuông góc với đường △ : y = 2x − 1.
A. m = 0
B. m = - 5 6
C. m < 5 6
D. m > - 1 2
Câu 1: Cho parabol (P):y=x^2+bx+c (b,c là các tham số thực)
a. Tìm giá trị của b,c biết parabol (P) đi qua điểm M(-3;2) và có trục đối xứng là đường thẳng x=-1
b. Với giá trị của b,c tìm được ở câu a), tìm m để đường thẳng d:y=-x-m cắt parabol(P) tại 2 điểm phân biệt A,B sao cho tam giác OAB vuông tại O( với O là gốc toạ độ)
Tìm tất cả các giá trị thực của m để hai đường thẳng d: y = mx − 3 và △ : y + x = m cắt nhau tại một điểm nằm trên trục hoành.
A. m = 3
B. m = ± 3
C. m = - 3
D. m = 3
Cho hai đường thẳng (d1): y −3x + m + 2; (d2): y 4x − 2m − 5. Gọi A (1;
y
A
) thuộc (d1), B (2;
y
B
) thuộc (d2). Tìm tất cả các giá trị của m để A và B nằm về hai phía của trục hoành. A.
m
1
m
3...
Đọc tiếp
Cho hai đường thẳng (d1): y = −3x + m + 2; (d2): y = 4x − 2m − 5. Gọi A (1; y A ) thuộc (d1), B (2; y B ) thuộc (d2). Tìm tất cả các giá trị của m để A và B nằm về hai phía của trục hoành.
A. m = 1 m = 3 2
B. m ∈ 1 ; + ∞ \ { 3 2 }
C. m ∈ − ∞ ; 3 2
D. m > 3 2 m < 1
Cho parabol \(\left(P\right):y=x^2+2x-3\)và đường thẳng \(\left(d\right):y=x+m\). Tìm tất cả giá trị m để (d) cắt (P) tại hai điểm phân biệt A, B nằm về hai phía của đường thẳng có phương trình y=1
Xác định tham số của giá trị m trong các trường hợp sau: a) (P): y= x^2+6x-3 và đường thẳng d: y= -2xm-m^2 cắt nhau tại 2 điểm phân biệt A,B sao cho biểu thức P= 5( xA+xB)-2xA.xB đạt giá trị lớn nhất b) (P): y= x^2-2x-2 và đường thẳng d: y= x+m cắt nhau tại 2 điểm phân biệt A,B sao cho OA^2+OB^2 đạt GTNN