Chọn C
Áp dụng công thức giải nhanh về khoảng cách
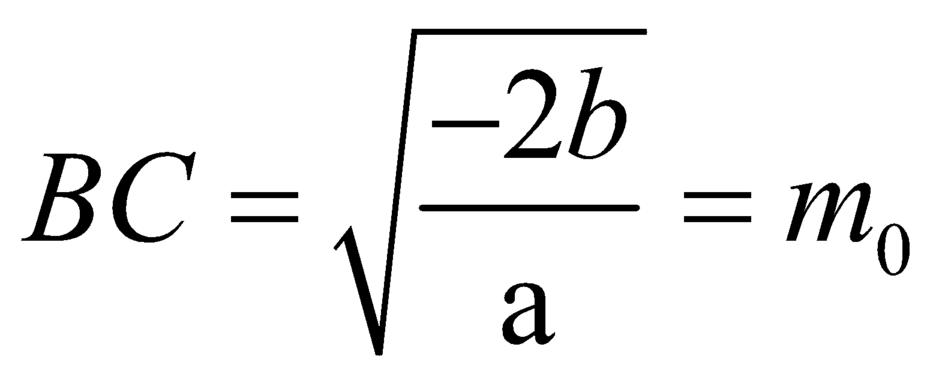 của hai điểm cực tiểu (hoặc hai điểm cực đại):
của hai điểm cực tiểu (hoặc hai điểm cực đại): ![]()
Chú ý: Các điểm cực trị đồ thị hàm số thuộc các trục tọa độ:
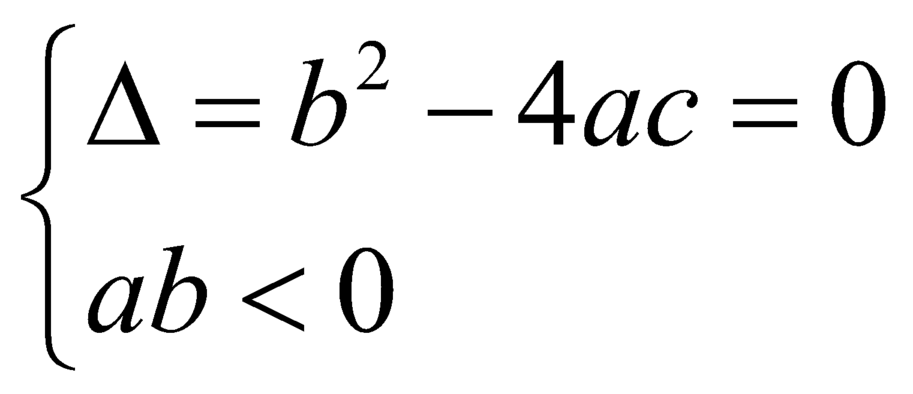
Chọn C
Áp dụng công thức giải nhanh về khoảng cách
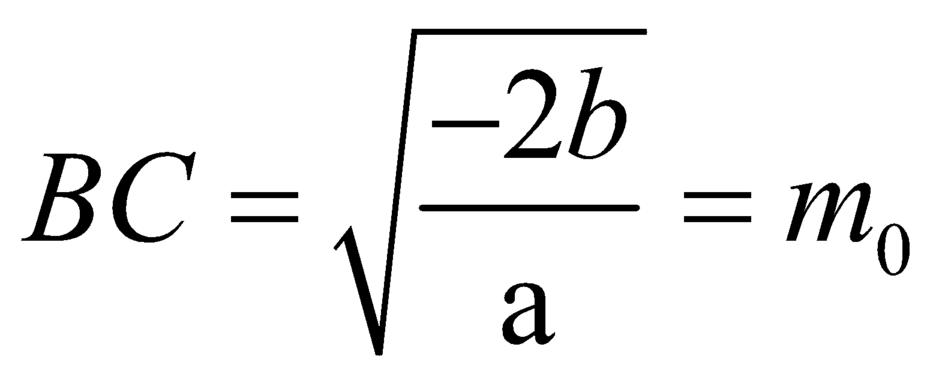 của hai điểm cực tiểu (hoặc hai điểm cực đại):
của hai điểm cực tiểu (hoặc hai điểm cực đại): ![]()
Chú ý: Các điểm cực trị đồ thị hàm số thuộc các trục tọa độ:
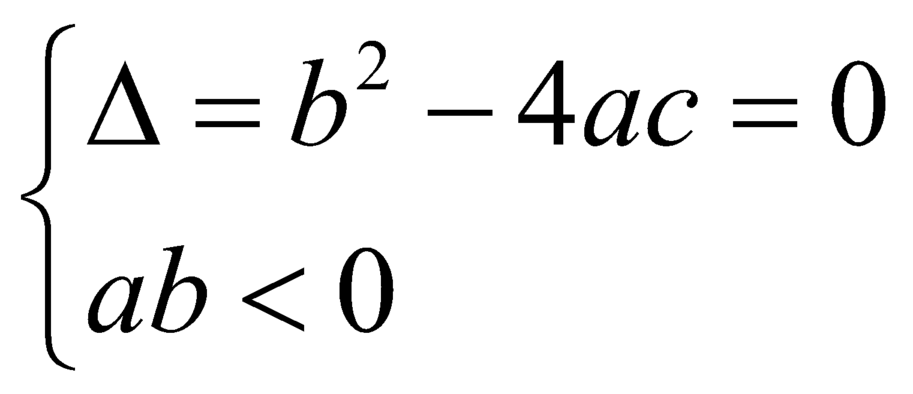
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 3 m x 2 + 3 ( m 2 - 1 ) x - m 3 + m có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng 2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O
A. m = - 3 - 2 2 h o ặ c m = - 1
B. m = - 3 + 2 2 h o ặ c m = - 1
C. m = - 3 + 2 2 h o ặ c m = - 3 - 2 2 .
D. m = - 3 + 2 2
Cho hàm số y=x4-2( m2-m+1)x2+m-1 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số có một điểm cực đại và hai điểm cực tiểu, đồng thời khoảng cách giữa hai điểm cực tiểu ngắn nhất.
A. m= -1/2
B. m= 1/2
C. m=2
D. m=1
Cho hàm số y= x4-2( m+1)x2+ m ( C). Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số C có ba điểm cực trị A: B; C sao cho OA= BC ; trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung, B và C là hai điểm cực trị còn lại.
A. m = 2 ± 2 2
B. m = 2 + 2 2
C. m = 2 - 2 2
D. m = ± 1
Cho hàm số y = x 4 - 2 ( m + 1 ) x 2 + m ( C ) . Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số (C) có ba điểm cực trị A, B, C sao cho OA = BC; trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung, B và C là hai điểm cực trị còn lại
A. m = 2 ± 2 2
B. m = 2 + 2 2
C. m = 2 - 2 2
D. m = ± 1
Tính tổng tất cả các giá trị thực của tham số m để hàm số y= x3-3mx2+ 3( m2-1) x- m3+ m có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng 2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O.
A. -4
B. -5
C. -6.
D. -7
Gọi S là tập tất cả các giá trị nguyên của tham số m để đồ thị hàm số y = − x 3 + 3 x 2 + 3 m 2 − 1 x − 3 m 2 − 1 có điểm cực đại và điểm cực tiểu, đồng thời khoảng cách giữa các điểm cực trị đó không vượt quá 30 13 . Số phần tử của tập hợp S là
A. 7
B. 4
C. 6
D. 5
Cho hàm số y = 2 x 3 + 3 m - 1 x 2 + 6 m - 2 x - 1 với m là tham số thực. Tìm tất cả các giá trị của m để hàm số có điểm cực đại và điểm cực tiểu nằm trong khoảng (-2; 3) .
A. m ∈ - 1 ; 3 ∪ 3 ; 4
B. (1; 3)
C. (3; 4)
D. (-1; 4)
Tìm tất cả các giá trị thực của tham số m để hàm số y = - x 3 + 3 x 2 + 3 m 2 - 1 x - 3 m 2 - 1 có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số cách đều gốc tọa độ O.
A. m = ± 1 2
B. m = 1 2
C. m = -1
D. m = ± 1