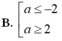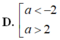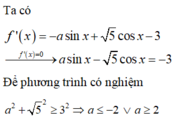Các câu hỏi tương tự
Tìm m để phương trình f‘(x) 0 có nghiệm. Biết f(x) m.cosx + 2.sinx – 3x + 1.
A
.
m
0
B
.
-
5
m
5
C
.
m
≥
5
D
....
Đọc tiếp
Tìm m để phương trình f‘(x) = 0 có nghiệm. Biết f(x) = m.cosx + 2.sinx – 3x + 1.
A . m > 0
B . - 5 < m < 5
C . m ≥ 5
D . m < 0
Tìm tất cả các giá trị thực của tham số m để phương trình sinx=m có nghiệm;
A. -1 ≤ m ≤1.
B. m ≤1.
C. m ≤-1.
D. m ≥-1.
Tìm tất cả giá trị của m để phương trình sin2x – 2( m- 1)sinx. cosx – (m- 1).cos2x = m có nghiệm?
A. 0 ≤ m ≤ 1
B.m> 1
C.0< m< 1
D. m ≤ 0
Tìm tất cả các giá trị của tham số thực m để phương trình 3 . sin x + m . cos x = 0 vô nghiệm.
A. m > 4
B. m < -4
C. - 4 < m < 4
D. tất cả đều sai
Tìm tất cả giá trị của tham số m để phương trình \(\left(sinx-2m+1\right)\left(2cosx-1\right)=0\)
a) Có 2 nghiệm thuộc \([-\dfrac{\pi}{2};\dfrac{5\pi}{6}]\)
b) Có 3 nghiệm thuộc \([-\dfrac{\pi}{2};\dfrac{5\pi}{6}]\)
Cho hàm số . Tìm tất cả các giá trị của tham số m để hàm số
y
f
(
x
)
có 5 điểm cực trị.
Đọc tiếp
Cho hàm số 
. Tìm tất cả các giá trị của tham số m để hàm số
y
=
f
(
x
)
có 5 điểm cực trị.
cho pt: \(x^2+3x+2m=0\)
và \(x^2+6x+5m=0\)
tìm tất cả giá trị m nguyên để 2 phương trình đều có 2 nghiệm phân biệt và giữa 2 nghiệm của pt này có đúng 1 nghiệm của pt kia
Tìm tất cả các giá trị của tham số m để phương trình:
cos
4
x
cos
2
3
x
+
m
sin
2
x
có nghiệm
x
∈
0
;
π
12
Đọc tiếp
Tìm tất cả các giá trị của tham số m để phương trình: cos 4 x = cos 2 3 x + m sin 2 x có nghiệm x ∈ 0 ; π 12
Tìm tất cả các giá trị thực của tham số m để phương trình
2
.
sin
2
x
-
(
2
m
+
1
)
.
sin
x
+
2
m
-
1
0
có nghiệm thuộc khoảng
-
π...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình 2 . sin 2 x - ( 2 m + 1 ) . sin x + 2 m - 1 = 0 có nghiệm thuộc khoảng - π 2 , 0 .
