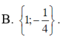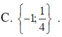Các câu hỏi tương tự
Gọi S là tập nghiệm của phương trình
2
(
2
x
-
1
)
-
5
.
2
(
x
-
1
)
+
3
0
.
Tìm S. A. S {1; log23 } B. S...
Đọc tiếp
Gọi S là tập nghiệm của phương trình 2 ( 2 x - 1 ) - 5 . 2 ( x - 1 ) + 3 = 0 . Tìm S.
A. S = {1; log23 }
B. S = {0; log 2 3 }
C. S = {1; log 3 2 }
D. S = {1}
Gọi S1 là tập nghiệm của bất phương trình
log
2
(
x
+
5
)
+
log
1
2
(
3
-
x
)
≥
0
và S2 là tập nghiệm của bất phương trình log2(x + 1) ≥ 1. Khẳng định nào dưới đây đúng ? A.
S
1
∩
S
2
[...
Đọc tiếp
Gọi S1 là tập nghiệm của bất phương trình log 2 ( x + 5 ) + log 1 2 ( 3 - x ) ≥ 0 và S2 là tập nghiệm của bất phương trình log2(x + 1) ≥ 1. Khẳng định nào dưới đây đúng ?
A. S 1 ∩ S 2 = [ 1 ; 3 )
B. S 1 ∩ S 2 = [ - 1 ; 3 )
C. S 1 ∩ S 2 = - 1 ; 1
D. S 1 ∩ S 2 = 1 ; 3
Cho F(x) là một nguyên hàm của hàm số
1
e
x
+
1
, thỏa mãn F(0) –ln2. Tìm tập nghiệm S của phương trình F(x) + ln(ex + 1) 3. A.
S
3
B.
S
-
3
C.
S...
Đọc tiếp
Cho F(x) là một nguyên hàm của hàm số 1 e x + 1 , thỏa mãn F(0) = –ln2. Tìm tập nghiệm S của phương trình F(x) + ln(ex + 1) = 3.
A. S = 3
B. S = - 3
C. S = ∅
D. S = ± 3
Tìm tập hợp nghiệm của phương trình 2 x 2 - x - 4 = 0
A. {1;2} B. {2;3}
C. {-2;3} D. {2;-3}
Tìm tập hợp nghiệm của phương trình 2 x 2 - x - 4 = 0
A. {1;2} B. {2;3}
C. {-2;3} D. {2;-3}
Gọi S là tập nghiệm của phương trình log5(x+1) + log5( x-3) 1. Tìm S A.S {-2; 4} B. C. S {4} D.
Đọc tiếp
Gọi S là tập nghiệm của phương trình log5(x+1) + log5( x-3) = 1. Tìm S
A.S= {-2; 4}
B. 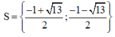
C. S= {4}
D. 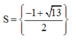
Tìm tập các giá trị thực của tham số m để phương trình
4
(
2
+
1
)
x
+
2
-
1
x
-
m
0
có đúng hai nghiệm âm phân biệt. A. (2;4) B. (3;5) C. (4;5) D. (5...
Đọc tiếp
Tìm tập các giá trị thực của tham số m để phương trình 4 ( 2 + 1 ) x + 2 - 1 x - m = 0 có đúng hai nghiệm âm phân biệt.
A. (2;4)
B. (3;5)
C. (4;5)
D. (5;6)
Tìm tập nghiệm S của phương trình
x
-
1
x
-
2
x
x
+
1
0
Đọc tiếp
Tìm tập nghiệm S của phương trình x - 1 x - 2 x x + 1 = 0
![]()
![]()
![]()
![]()
Cho phương trình
m
.
l
n
2
(
x
+
1
)
-
(
x
+
2
-
m
)
l
n
(
x
+
1
)
-
x
-
2
0
(1). Tập hợp tất cả các giá trị của tham số m để phương trình (1) có hai nghiệm phân biệt thoả mãn
0...
Đọc tiếp
Cho phương trình m . l n 2 ( x + 1 ) - ( x + 2 - m ) l n ( x + 1 ) - x - 2 = 0 (1). Tập hợp tất cả các giá trị của tham số m để phương trình (1) có hai nghiệm phân biệt thoả mãn 0 < x 1 < 2 < 4 < x 2 là khoảng . Khi đó a thuộc khoảng
![]()
![]()
![]()
![]()
Kí hiệu F(x) là một nguyên hàm của hàm số
f
(
x
)
1
e
x
+
1
, biết F(0) -ln2. Tìm tập nghiệm S của phương trình A. S {-3;3} B. S {3} C.
S
∅
D. S {-3}
Đọc tiếp
Kí hiệu F(x) là một nguyên hàm của hàm số f ( x ) = 1 e x + 1 , biết F(0) = -ln2. Tìm tập nghiệm S của phương trình
A. S = {-3;3}
B. S = {3}
C. S = ∅
D. S = {-3}