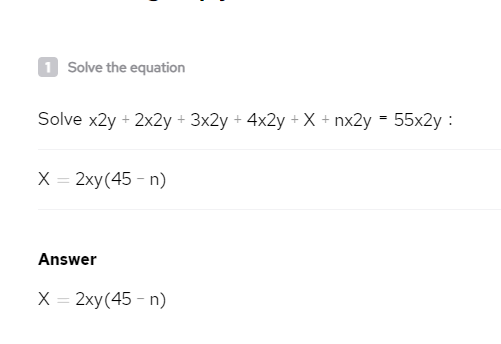x2y + 2x2y + 3x2y + 4x2y + .... + nx2y = 55x2y
\(\Rightarrow x^2y\left(1+2+...+n\right)=55x^2y\)
\(\Rightarrow1+2+...+n=55\)
\(\Rightarrow\dfrac{\left(\dfrac{n-1}{1}+1\right).\left(n+1\right)}{2}=55\)
\(\Rightarrow n\left(n+1\right)=55.2=110\)
\(\Rightarrow n^2+n-110=0\)
\(\Rightarrow n^2-10n+11n-110=0\)
\(\Rightarrow n\left(n-10\right)+11\left(n-10\right)=0\)
\(\Rightarrow\left(n-10\right)\left(n+11\right)=0\)
\(\Rightarrow n-10=0\) hay \(n+11=0\)
\(\Rightarrow n=10\left(nhận\right)\) hay \(n=-11\left(loại\right)\)
Đúng 2
Bình luận (0)
