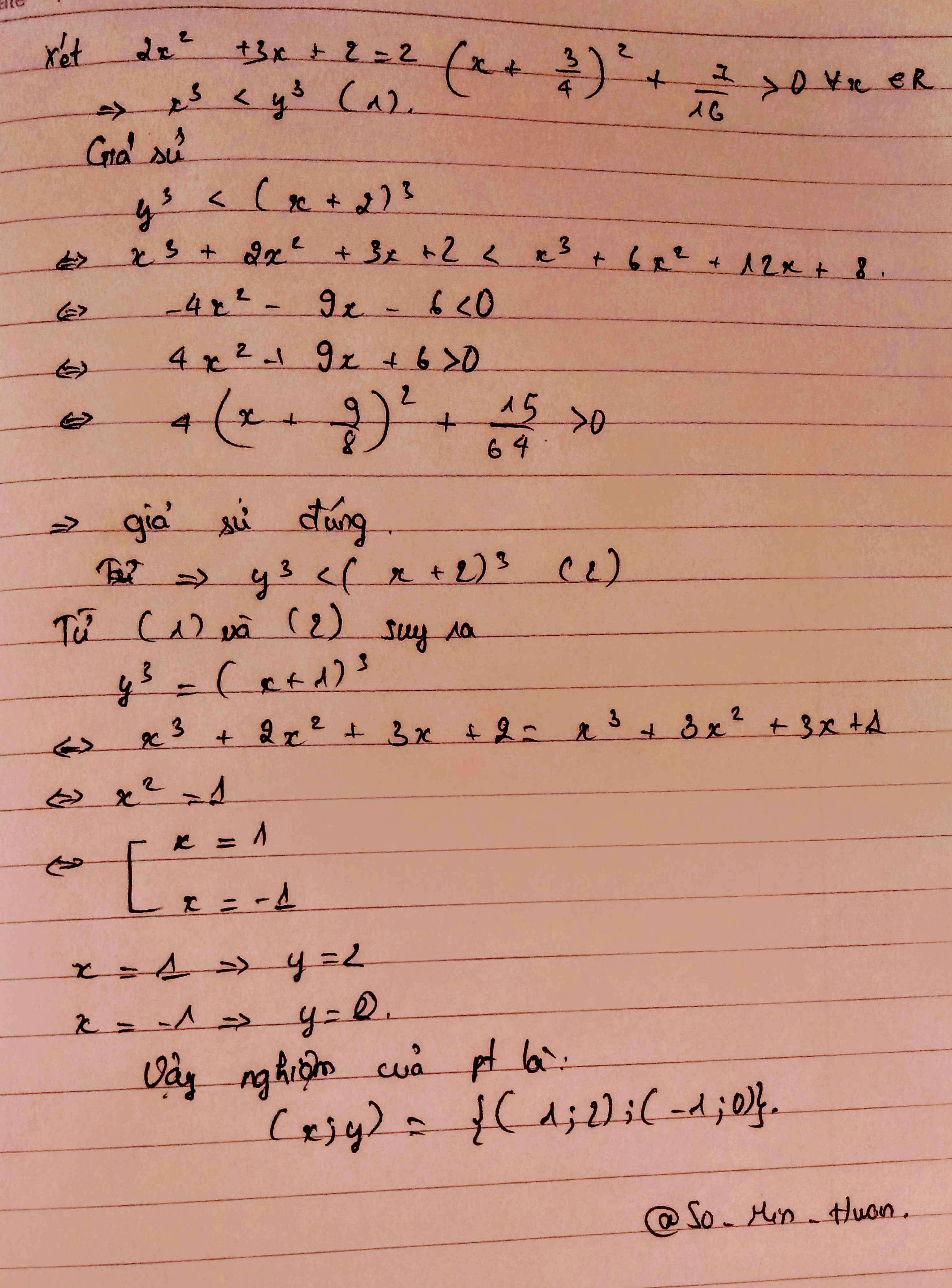Xét \(2x^2+3x+2=2\left(x+\dfrac{3}{4}\right)^2+\dfrac{7}{16}>0\forall x\in Z\)
\(\Rightarrow x^3< y^3\left(1\right)\)
Giả sử : \(y^3< \left(x+2\right)^3\)
\(\Rightarrow x^3+2x^2+3x+2< x^3+6x^2+12x+8\)
\(\Rightarrow-4x^2-9x-6< 0\)
\(\Rightarrow4x^2+9x+6>0\)
\(\Rightarrow4\left(x+\dfrac{9}{8}\right)^2+\dfrac{15}{64}>0\)
Giả sử đúng : \(\Rightarrow y^3< \left(x+2\right)^3\left(2\right)\)
Từ (1) và (2) => \(y^3=\left(x+1\right)^3\)
\(\Rightarrow x^3+2x^2+3x+2=x^3+3x^2+3x+1\)
\(\Rightarrow x^2=1\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=1\Rightarrow y=2\\x=-1\Rightarrow y=0\end{matrix}\right.\)