Các câu hỏi tương tự
Cho số phức z thỏa mãn
z
.
z
2
và
z
-
2
-
1
-
z
là một số ảo. Tích trị tuyệt đối phần thực và phần ảo của z là
Đọc tiếp
Cho số phức z thỏa mãn z . z = 2 và z - 2 - 1 - z là một số ảo. Tích trị tuyệt đối phần thực và phần ảo của z là
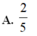
![]()
Phần thực và phần ảo của số phức z thỏa mãn: (1 + i)2(2 - i) z = 8 + i + (1 + 2i)z lần lượt là?
A. -3; -2
B. 2; 3
C. 2; -3
D. Đáp án khác.
Trên mặt phẳng tọa độ tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện:
a) Phần thực của z bằng phần ảo của nó ;
b) Phần thực của z là số đối của phần ảo của nó ;
c) Phần ảo của z bằng hai lần phần thực của nó cộng với 1;
d) Modun của z bằng 1, phần thực của z không âm.
Cho số phức z thỏa mãn
5
z
+
i
2
-
i
z
+
1
. Gọ...
Đọc tiếp
Cho số phức z thỏa mãn 5 z + i = 2 - i z + 1 . Gọi a, b lần lượt là phần thực và phần ảo của số phức 1 + z + z 2 , tổng a+b bằng
A. 13
B. -5
C. 9
D. 5
Cho số phức z(1-2i)(4-3i)-2+8i. Cho các phát biểu sau: (1) Modun của z là một số nguyên tố (2) z có phần thực và phần ảo đều âm (3) z là số thuần thực (4) Số phức liên hợp của z có phần ảo là 3i Số phát biểu sai là: A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Cho số phức z=(1-2i)(4-3i)-2+8i. Cho các phát biểu sau:
(1) Modun của z là một số nguyên tố
(2) z có phần thực và phần ảo đều âm
(3) z là số thuần thực
(4) Số phức liên hợp của z có phần ảo là 3i
Số phát biểu sai là:
A. 1
B. 2
C. 3
D. 4
Gọi z là số phức có môđun nhỏ nhất và thỏa mãn
z
+
1
+
i
z
¯
+
i
. Tổng phần thực và phần ảo của số phức z bằng
Đọc tiếp
Gọi z là số phức có môđun nhỏ nhất và thỏa mãn z + 1 + i = z ¯ + i . Tổng phần thực và phần ảo của số phức z bằng
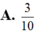
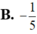
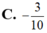
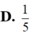
Phần thực và phần ảo của số phức z=(1+2i)i lần lượt là
A. 1 và 2.
B. -2 và 1.
C. 1 và -2.
D. 2 và 1
Phần thực và phần ảo của số phức z=(1+2i)i lần lượt là
A. 1 và 2.
B.-2 và 1.
C. 1 và -2.
D. 2 và 1
Nếu a ,b lần lượt là phần thực và phần ảo của số phức z1-i thì A. . B. . C. . D.
Đọc tiếp
Nếu a ,b lần lượt là phần thực và phần ảo của số phức z=1-i thì
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]()