Các câu hỏi tương tự
Tính tích phân Iintlimits^{pi}_0x^2cos2xdx bằng cách đặt left{{}begin{matrix}ux^2dvcos2xdxend{matrix}right..Mệnh đề nào dưới đây đúng?A. Idfrac{1}{2}x^2sin2x|^{^{pi}_0}-intlimits^{pi}_0xsin2xdxB. Idfrac{1}{2}x^2sin2x|^{^{pi}_0}-2intlimits^{pi}_0xsin2xdxC. Idfrac{1}{2}x^2sin2x|^{^{pi}_0}+intlimits^{pi}_0xsin2xdxD. Idfrac{1}{2}x^2sin2x|^{^{pi}_0}+2intlimits^{pi}_0xsin2xdx
Đọc tiếp
Tính tích phân I=\(\int\limits^{\pi}_0\)\(x^2cos2xdx\) bằng cách đặt \(\left\{{}\begin{matrix}u=x^2\\dv=cos2xdx\end{matrix}\right.\).Mệnh đề nào dưới đây đúng?
A. \(I=\dfrac{1}{2}x^2sin2x|^{^{\pi}_0}-\int\limits^{\pi}_0xsin2xdx\)
B. \(I=\dfrac{1}{2}x^2sin2x|^{^{\pi}_0}-2\int\limits^{\pi}_0xsin2xdx\)
C. \(I=\dfrac{1}{2}x^2sin2x|^{^{\pi}_0}+\int\limits^{\pi}_0xsin2xdx\)
D. \(I=\dfrac{1}{2}x^2sin2x|^{^{\pi}_0}+2\int\limits^{\pi}_0xsin2xdx\)
Cho hàm số y f(x) liên tục trên [a;b] Giả sử hàm số u u(x) có đạo hàm liên tục trên [a;b] và
u
(
x
)
∈
[
a
;
b
]
hơn nữa u(x) liên tục trên đoạn [a;b]Mệnh đề nào sau đây là đúng?
Đọc tiếp
Cho hàm số y = f(x) liên tục trên [a;b] Giả sử hàm số u = u(x) có đạo hàm liên tục trên [a;b] và u ( x ) ∈ [ a ; b ] hơn nữa u(x) liên tục trên đoạn [a;b]Mệnh đề nào sau đây là đúng?
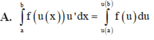
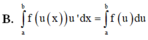
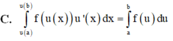

Cho số phức u và v. Xét các mệnh đề dưới đây1.
u
+
v
u
+
v
2.
u
−
v
u
−
v
3.
u
.
v
u
.
v
4. ...
Đọc tiếp
Cho số phức u và v. Xét các mệnh đề dưới đây
1. u + v = u + v
2. u − v = u − v
3. u . v = u . v
4. u v = u v v ≠ 0
Hỏi có bao nhiêu mệnh đề đúng trong 4 mệnh đề trên?
A. 1
B. 2
C. 3
D. 4
Cho
I
1
2
∫
0
1
x
1
+
2
x
d
x
và
u
2
x
+
1
Mệnh đề nào dưới đây sai?
Đọc tiếp
Cho I = 1 2 ∫ 0 1 x 1 + 2 x d x và u = 2 x + 1 Mệnh đề nào dưới đây sai?
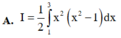
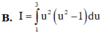
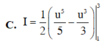
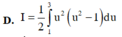
Khi tính nguyên hàm
∫
x
-
3
x
+
1
dx , bằng cách đặt
u
x
+
1
ta được nguyên hàm nào?
Đọc tiếp
Khi tính nguyên hàm ∫ x - 3 x + 1 dx , bằng cách đặt u = x + 1 ta được nguyên hàm nào?
![]()
![]()
![]()
![]()
Cho tích phân
I
∫
0
1
2
x
+
1
2
d
x
1. Tính I bằng cách khai triển
2
x
+
1
2
.2. Đặt u 2x + 1. Biến đổi biểu thức ...
Đọc tiếp
Cho tích phân I = ∫ 0 1 2 x + 1 2 d x
1. Tính I bằng cách khai triển 2 x + 1 2 .
2. Đặt u = 2x + 1. Biến đổi biểu thức 2 x + 1 2 dx thành g(u)du.
3. Tính ∫ u 0 u 1 g u d u và so sánh kết quả với I trong câu 1
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
Cho hàm số
y
x
+
2
1
-
x
2
. Xét các mệnh đề sau đây: (I). Hàm số có tập xác định D(-1;1). (II). Đồ thị hàm số có 2 đường tiệm cận ngang là y1 và y-1. (III). Đồ thị hàm số có 2 đường tiệm cận đứng là x1 và x-1...
Đọc tiếp
Cho hàm số y = x + 2 1 - x 2 . Xét các mệnh đề sau đây:
(I). Hàm số có tập xác định D=(-1;1).
(II). Đồ thị hàm số có 2 đường tiệm cận ngang là y=1 và y=-1.
(III). Đồ thị hàm số có 2 đường tiệm cận đứng là x=1 và x=-1.
(IV). Hàm số có một cực trị.
Số mệnh đề đúng là:
A.3
B.1
C.2
D.4
Trong không gian Oxy cho điểm A(-1;2;3), véc-tơ
u
→
6
;
−
2
;
−
3
và đường thẳng d:
x
−
4
3
y
+
1
2
z...
Đọc tiếp
Trong không gian Oxy cho điểm A(-1;2;3), véc-tơ u → 6 ; − 2 ; − 3 và đường thẳng d: x − 4 3 = y + 1 2 = z + 2 − 5 . Viết phương trình đường thẳng ∆ đi qua A, vuông góc ới giá của u → và cắt d
A. x − 1 2 = y + 1 − 3 = z − 3 6
B. x − 1 2 = y − 5 3 = z + 1 2
C. x − 1 1 = y + 4 − 3 = z − 5 4
D. x − 2 3 = y − 5 3 = z − 1 4