Chọn D
Vì x 4 + x 2 + 1 ≥ 0 , ∀ x ∈ - 1 ; 2018
⇒ ∫ - 1 2018 x 4 + x 2 + 1 d x = ∫ - 1 2018 ( x 4 + x 2 + 1 ) d x
Chọn D
Vì x 4 + x 2 + 1 ≥ 0 , ∀ x ∈ - 1 ; 2018
⇒ ∫ - 1 2018 x 4 + x 2 + 1 d x = ∫ - 1 2018 ( x 4 + x 2 + 1 ) d x
Cho f(x) là hàm số liên tục trên đoạn [a; b] và c ∈ a ; b . Tìm mệnh đề đúng trong các mệnh đề sau.
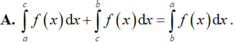
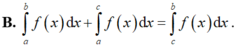
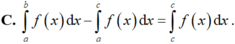
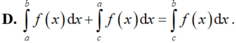
Gọi F(x) là nguyên hàm trên R của hàm số f ( x ) = x 2 e a x ( a ≠ 0 ) sao cho F 1 a = F ( 0 ) + 1 . Chọn mệnh đề đúng trong các mệnh đề sau.
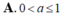
![]()
![]()
![]()
Cho hàm số y = f x xác định, có đạo hàm trên đoạn a ; b (với a < b ). Xét các mệnh đề sau:
i) Nếu f ' x > 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) đồng biến trên khoảng a ; b .
ii) Nếu phương trình f ' ( x ) = 0 có nghiệm x 0 thì f ' ( x ) đổi dấu từ dương sang âm khi qua x 0 .
iii) Nếu f ' x ≤ 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) nghịch biến trên khoảng a ; b .
Số mệnh đề đúng trong các mệnh đề trên là:
A. 2
B. 3
C. 0
D. 1
Cho a, b, c là các số thực dương, a ≠ 1 . Xét các mệnh đề sau:
(I) 2 a = 3 ⇔ a = log 2 3
(II) ∀ x ∈ ℝ \ 0 , log 3 x 2 = 2 log 3 x
(III) log a b . c = log a b . log a c
Trong ba mệnh đề (I), (II), (III), tổng số mệnh đề đúng là?
A. 3
B. 2
C. 1
D. 0
Cho a; b > 0 và a , b ≠ 1 , x và y là hai số thực dương. Tìm mệnh đề đúng trong các mệnh đề sau:
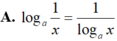
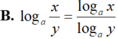
![]()
![]()
Trong không gian Oxyz, cho hai đường thẳng d : x - 1 2 = y - 7 1 = z - 3 4 và d ' : x - 6 3 = y + 1 - 2 = z + 2 1 . Trong các mệnh đề sau, mệnh đề nào đúng?
A. Song song.
B. Trùng nhau.
C. Cắt nhau.
D. Chéo nhau.
Trong không gian Δ, cho hai đường thẳng d : x - 1 2 = y - 7 1 = z - 3 4 v à d ' : x - 6 3 = y + 1 - 2 = z + 2 1 . Trong các mệnh đề sau, mệnh đề nào đúng?
A. Song song.
B. Trùng nhau.
C. Cắt nhau.
D. Chéo nhau.
Cho các số thực a, b và các mệnh đề:
1 . ∫ a b f ( x ) d x = - ∫ a b f ( x ) d x
2 . ∫ a b 2 f ( x ) d x = 2 ∫ a b f x d x
3 . ∫ a b f 2 x d x = ∫ a b f x d x 2
4 . ∫ a b f x d x = ∫ a b f u d u
Số mệnh đề đúng trong 4 mệnh đề trên là:
A. 3.
B. 4
C. 2
D. 1
Cho hàm số y = f(x) có đạo hàm trong khoảng (a, b) chứa điểm x0 (có thể trừ điểm x0). Tìm mệnh đề đúng trong các mệnh đề sau:
A. Nếu f(x) không có đạo hàm tại x0 thì f(x) không đạt cực trị tại x0
B. Nếu f’(x0) = 0 thì f(x) đạt cực trị tại điểm x0
C. Nếu f’(x0) = 0 và f’’(x0) = 0 thì f(x) không đạt cực trị tại điểm x0
D. Nếu f’(x0) = 0 và f’’(x0) ≠ 0 thì f(x) đạt cực trị tại điểm x0