Các câu hỏi tương tự
Tìm tất cả các nghiệm thực của tham số m để phương trình mx2 + 2(m + 1)x + m 0 có hai nghiệm phân biệt. A.
m
≠
0
m
-
1
2
B. ...
Đọc tiếp
Tìm tất cả các nghiệm thực của tham số m để phương trình mx2 + 2(m + 1)x + m = 0 có hai nghiệm phân biệt.
A. m ≠ 0 m > - 1 2
B. m > 1 2
C. m > - 1 2
D. m > 0
Tìm tập các giá trị thực của tham số m để phương trình
4
(
2
+
1
)
x
+
2
-
1
x
-
m
0
có đúng hai nghiệm âm phân biệt. A. (2;4) B. (3;5) C. (4;5) D. (5...
Đọc tiếp
Tìm tập các giá trị thực của tham số m để phương trình 4 ( 2 + 1 ) x + 2 - 1 x - m = 0 có đúng hai nghiệm âm phân biệt.
A. (2;4)
B. (3;5)
C. (4;5)
D. (5;6)
Cho phương trình
m
.
l
n
2
(
x
+
1
)
-
(
x
+
2
-
m
)
l
n
(
x
+
1
)
-
x
-
2
0
(1). Tập hợp tất cả các giá trị của tham số m để phương trình (1) có hai nghiệm phân biệt thoả mãn
0...
Đọc tiếp
Cho phương trình m . l n 2 ( x + 1 ) - ( x + 2 - m ) l n ( x + 1 ) - x - 2 = 0 (1). Tập hợp tất cả các giá trị của tham số m để phương trình (1) có hai nghiệm phân biệt thoả mãn 0 < x 1 < 2 < 4 < x 2 là khoảng . Khi đó a thuộc khoảng
![]()
![]()
![]()
![]()
Tìm tất cả các giá trị của m để phương trình
log
2
3
x
−
2
−
log
2
3
x
+
1
m
có 3 nghiệm phân biệt? A. m 3. B. m 2. C. m 0. D. m 2.
Đọc tiếp
Tìm tất cả các giá trị của m để phương trình log 2 3 x − 2 − log 2 3 x + 1 = m có 3 nghiệm phân biệt?
A. m > 3.
B. m < 2.
C. m > 0.
D. m = 2.
Cho phương trình
4
x
2
-
2
x
+
1
-
m
.
2
x
2
-
2
x
+
2
+
3
m
-
2
0...
Đọc tiếp
Cho phương trình 4 x 2 - 2 x + 1 - m . 2 x 2 - 2 x + 2 + 3 m - 2 = 0 với m là tham số thực. Tìm tất cả các giá trị của m để phương trình có bốn nghiệm phân biệt.
A. m < 1
B. m < 1; m > 2
C. m ≥ 2
D. m > 2
Phương trình
2
x
-
2
+
m
+
3
x
3
+
x
3
-
6...
Đọc tiếp
Phương trình 2 x - 2 + m + 3 x 3 + x 3 - 6 x 2 + 9 x + m . 2 x - 2 = 2 x + 1 + 1 có 3 nghiệm phân biệt khi và chỉ khi m ∈ a ; b . Đặt T = b 2 - a 2 thì
A. T = 36.
B. T = 48.
C. T = 64.
D. T = 72.
Cho hàm số \(y=\dfrac{1}{2}x^4-x^2+m\)(m là tham số ) có đồ thị (Cm), đường tròn (S)có phương trình \(x^2+y^2+2x+6y+1=0\) và điểm A(-1;-6).Tìm m để tồn tại tiếp tuyến với đồ thị (Cm) cắt đường tròn (S) tại hai điểm phân biệt B,C sao cho tam giác ABC có chu vi đạt giá trị lớn nhất
Cho hàm số
f
(
x
)
-
4
x
4
+
8
x
2
-
1
.
Có bao nhiêu giá trị nguyên dương của m để phương trình f(x)m có đúng 2 nghiệm phân biệt A. 3 B. 0 C. 2 D. 1
Đọc tiếp
Cho hàm số f ( x ) = - 4 x 4 + 8 x 2 - 1 . Có bao nhiêu giá trị nguyên dương của m để phương trình f(x)=m có đúng 2 nghiệm phân biệt
A. 3
B. 0
C. 2
D. 1
Tìm tất cả giá trị thực của tham số m để phương trình
x
3
-
3
x
2
+
2
-
m
1
có 6 nghiệm phân biệt.
Đọc tiếp
Tìm tất cả giá trị thực của tham số m để phương trình x 3 - 3 x 2 + 2 - m = 1 có 6 nghiệm phân biệt.
![]()
![]()
![]()
![]()
Cho hàm số yf(x) liên tục trên tập Rvà có đồ thị (C) như hình vẽ. Có bao nhiêu giá trị nguyên dương của tham số m để phương trình
f
2
(
x
)
-
(
m
-
1
)
f
(
x
)
+
m
-
2
có 12 nghiệm phân biệt?
Đọc tiếp
Cho hàm số y=f(x) liên tục trên tập Rvà có đồ thị (C) như hình vẽ. Có bao nhiêu giá trị nguyên dương của tham số m để phương trình
f
2
(
x
)
-
(
m
-
1
)
f
(
x
)
+
m
-
2
có 12 nghiệm phân biệt?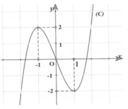
![]()
![]()
![]()
![]()