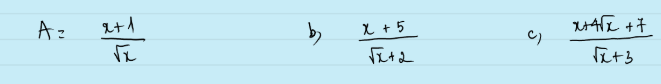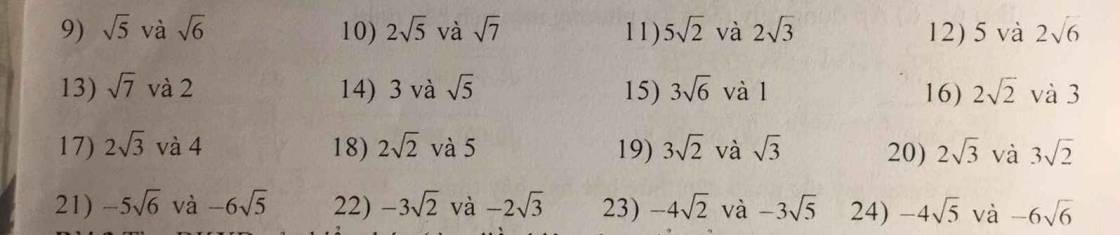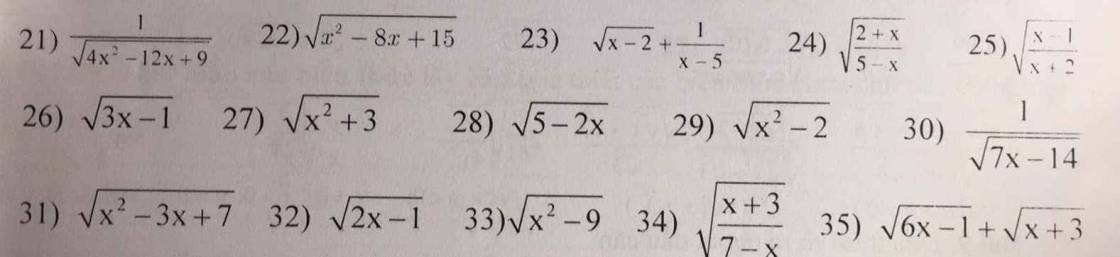\(A=\sqrt{x}+\dfrac{1}{\sqrt{x}}\ge2\sqrt{\sqrt{x}\cdot\dfrac{1}{\sqrt{x}}}=2\\ A_{min}=2\Leftrightarrow x=1\\ B=\dfrac{x-4+9}{\sqrt{x}+2}=\sqrt{x}-2+\dfrac{9}{\sqrt{x}+2}\\ B=\sqrt{x}+2+\dfrac{9}{\sqrt{x}+2}+4\ge2\sqrt{\left(\sqrt{x}+2\right)\cdot\dfrac{9}{\sqrt{x}+2}}+4\\ B\ge2\sqrt{9}+4=10\\ B_{min}=10\Leftrightarrow\sqrt{x}+2=3\left(\sqrt{x}+2\ge2\right)\Leftrightarrow x=1\)
Cho x>1/4 Tìm GTNN của biểu thức :
A= [2x- ( cănx)+8]/[2×(cănx)-1]
Các bạn giúp mình với mình đang cần gấp ♡♡♡♡
Tìm GTLN GTNN của biểu thức
M=
\(\frac{1}{3-\sqrt{1-X^2}}\)
Giúp mình với mình đang cần gấp
Giúp mk vs mk đg cần gấp!!!
Cho `x,y,z>0` thỏa mãn `x+y+z<=3/2`. Tìm GTNN của biểu thức `A=x^2+y^2+z^2+1/x+1/y+1/z.`
(Sử dụng BĐT Cosi)
giúp mình bài này vs ạ
bài 1:so sánh các căn sau
bài 2 :tìm ĐKXĐ của biểu thức (tìm đk của x để biểu thức sau có nghĩa)
Cho biểu thức:
\(Q=\frac{x^2-\sqrt{x}}{x+\sqrt{x}+1}-\frac{2x+\sqrt{x}}{\sqrt{x}}+\frac{2\left(x-1\right)}{\sqrt{x}-1}\)
a) Rút gọn Q
b) Tìm GTNN của Q
c) Tìm các số nguyên x để \(\frac{3Q}{\sqrt{x}}\) nhận giá trị nguyên
Giúp mk vs ạ, mình cần gấp
1.chứng minh rằng biểu thức sau không phụ thuộc vào biến: 2( sin6a + cos6a ) - 3( sin4a + cos4a)
2. tìm GTNN: sin4a + cos4a
3. tìm GTLN: cos a * sin a
ai đó giúp mình với. mình đang cần gấp lắm!!!
Cho x là số thực dương. Tìm GTNN của biểu thức \(A=9x+\frac{1}{9x}-\frac{6\sqrt{x}+8}{x+1}+2020\)
P/S: Các bạn và thầy cô giúp mình vs ạ...!
Cho x,y,z > 0 và xy + 2xz + 2yz = 65. Tìm GTNN của biểu thức A = 9x2 + 9y2 + 50z2
Giải giúp mình với ạ, đang cần gấp
Cho hai số x,y có tổng bằng 2. Tìm GTNN của biểu thức P=x^4+y^4
E cần gấp, Giúp e với ạ <3
