\(f\left(x\right)=x+\dfrac{1}{x}+1\ge2\sqrt{x.\dfrac{1}{x}}+1=3\)
\(\Rightarrow f\left(x\right)_{min}=3\) khi \(x=\dfrac{1}{x}\Rightarrow x=1\)
\(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=+\infty\) nên hàm ko tồn tại GTLN
Tìm GTLN (max), GTNN (min) của hàm số y = x + 2 x với x ∈ 1 ; 3
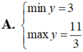
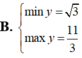
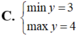
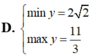
Tìm GTLN (max); GTNN (min) của hàm số y = 2 x + 1 + 4 - x .
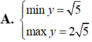
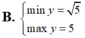
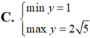
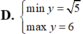
Tìm GTLN (max), GTNN (min) của hàm số y = x + 2 x 2 + 1 trên - 1 ; 1
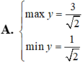
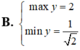
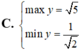
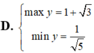
Tìm GTNN (min y) của hàm số y = log 3 x 2 + x + 1 - log 3 x với x > 0.
A. 0
B. 1
C. 1 2
D. 1 3
Tìm GTLN (max), GTNN (min) của hàm số y = x 3 - 2 x 2 - 4 x + 8 khi x ∈ - 1 ; 1
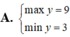
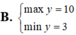
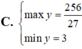
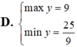
Cho F(x) là một nguyên hàm của hàm số f ( x ) = x x + 1 .Tìm F(x) biết F(0)=0.
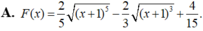
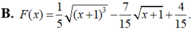
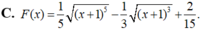
Cho hàm số y = x 2 - 2 | x | + 2 và các mệnh đề
(1) Hàm số trên liên tục trên R
(2) Hàm số trên có đạo hàm tại x = 0
(3) Hàm số trên đạt GTNN tại x = 0.
(4) Hàm số trên đạt GTLN tại x = 0.
(5) Hàm số trên là hàm chẵn
(6) Hàm số trên cắt trục hoành tại duy nhất một điểm
Trong các mệnh đề trên, số mệnh đề đúng là
A. 1
B. 2
C. 3
D. 4
Tìm một nguyên hàm F(x) của hàm số f x = a x + b x 2 ( x ≠ 0 ) . Biết rằng F(-1)=1, F(1)=4, f(1)=0.
Tìm hàm số f(x) thỏa mãn 3 x 2 . f ' ( x ) + x 3 . f ' ( x ) = - 1 với x ≠ 0 và f(1) = 1, f(-2) = -1
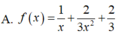
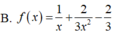
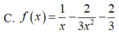
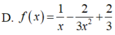
Cho hàm số y=f(x) có f'(x)>0 với mọi x. Tìm tập hợp tất cả các giá trị thực của x để f 1 x < f(1)
A. 
B. 
C. 
D. 
