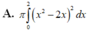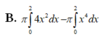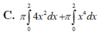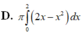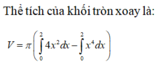Các câu hỏi tương tự
Cho hình phẳng (D) được giới hạn bởi các đường x0, x1, y0 và
y
2
x
+
1
.Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức
Đọc tiếp
Cho hình phẳng (D) được giới hạn bởi các đường x=0, x=1, y=0 và y = 2 x + 1 .Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức
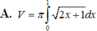
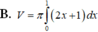
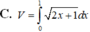
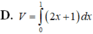
Cho hình phẳng (D) được giới hạn bởi các đường x 0; x 1; y 0 và
y
2
x
+
1
. Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục OX được tính theo công thức
Đọc tiếp
Cho hình phẳng (D) được giới hạn bởi các đường x = 0; x = 1; y = 0 và y = 2 x + 1 . Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục OX được tính theo công thức
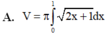
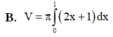
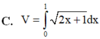
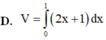
Thể tích của khối tròn xoay do hình phẳng giới hạn bởi các đường
y
x
, trục Ox và hai đường thẳng x1; x4 khi quay quanh trục hoành được tính bởi công thức nào?
Đọc tiếp
Thể tích của khối tròn xoay do hình phẳng giới hạn bởi các đường y = x , trục Ox và hai đường thẳng x=1; x=4 khi quay quanh trục hoành được tính bởi công thức nào?
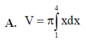
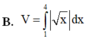
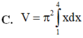
Cho hình phẳng (H) giới hạn bởi trục hoành, đồ thị của một parabol và một đường thẳng tiếp xúc parabol đó tại điểm A(2;4) như hình vẽ bên. Tính thể tích khối tròn xoay tạo bởi hình phẳng (H) khi quay xung quanh trục Ox. A.
32
π
5
B.
16
π
15
C.
22
π...
Đọc tiếp
Cho hình phẳng (H) giới hạn bởi trục hoành, đồ thị của một parabol và một đường thẳng tiếp xúc parabol đó tại điểm A(2;4) như hình vẽ bên. Tính thể tích khối tròn xoay tạo bởi hình phẳng (H) khi quay xung quanh trục Ox.
A. 32 π 5
B. 16 π 15
C. 22 π 5
D. 2 π 3
Cho hình phẳng (D) được giới hạn bởi các đường x0;
x
π
; y 0 và y -sinx. Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức:
Đọc tiếp
Cho hình phẳng (D) được giới hạn bởi các đường x=0; x = π ; y = 0 và y = -sinx. Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức:
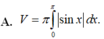
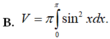
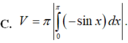
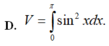
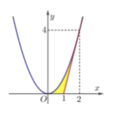
Tính thể tích khối tròn xoay được tạo thành khi quay hình phẳng (H) được giới hạn bởi các đường y f(x)trục Ox và hai đường thẳng x a; x b xung quanh trục Ox.
Đọc tiếp
Tính thể tích khối tròn xoay được tạo thành khi quay hình phẳng (H) được giới hạn bởi các đường y = f(x)trục Ox và hai đường thẳng x = a; x = b xung quanh trục Ox.
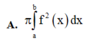
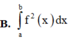
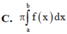
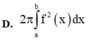
Gọi (D) là hình phẳng giới hạn bởi các đường
y
2
x
,
y
0
,
x
0
v
à
x
2
. Thể tích V của khối tròn xoay tạo thành khi quay (D) quanh trục Ox được xác định bởi công thức: A.
V
π
∫
0
2...
Đọc tiếp
Gọi (D) là hình phẳng giới hạn bởi các đường y = 2 x , y = 0 , x = 0 v à x = 2 . Thể tích V của khối tròn xoay tạo thành khi quay (D) quanh trục Ox được xác định bởi công thức:
A. V = π ∫ 0 2 2 x + 1 d x
B. V = ∫ 0 2 2 x + 1 d x
C. V = ∫ 0 2 4 x d x
D. V = π ∫ 0 2 4 x d x
Gọi D là hình phẳng giới hạn bởi đồ thị của hàm số
y
x
e
x
và các đường thẳng x1; x2; y0. Tính thể tích V của khối tròn xoay thu được khi quay hình D xung quanh trục Ox.
Đọc tiếp
Gọi D là hình phẳng giới hạn bởi đồ thị của hàm số y = x e x và các đường thẳng x=1; x=2; y=0. Tính thể tích V của khối tròn xoay thu được khi quay hình D xung quanh trục Ox.
![]()
![]()
![]()
![]()
Tính thể tích V của khối tròn xoay thu được khi quay xung quanh trục Ox hình phẳng giới hạn bởi các đường ytanx; x0;
x
π
3
và trục hoành.
Đọc tiếp
Tính thể tích V của khối tròn xoay thu được khi quay xung quanh trục Ox hình phẳng giới hạn bởi các đường y=tanx; x=0; x = π 3 và trục hoành.
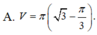
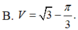

![]()