Giải
Ta có: ∆ACB = ∆ ECD(c.g.c)
∆ACD = ∆ECB(c.g.c)
∆ABD = ∆EDB(c.g.c)
∆ABE = ∆EDA(c.g.c)
Ta có: ∆ACB = ∆ ECD(c.g.c)
∆ACD = ∆ECB(c.g.c)
∆ABD = ∆EDB(c.g.c)
∆ABE = ∆EDA(c.g.c)

Giải
Ta có: ∆ACB = ∆ ECD(c.g.c)
∆ACD = ∆ECB(c.g.c)
∆ABD = ∆EDB(c.g.c)
∆ABE = ∆EDA(c.g.c)
Ta có: ∆ACB = ∆ ECD(c.g.c)
∆ACD = ∆ECB(c.g.c)
∆ABD = ∆EDB(c.g.c)
∆ABE = ∆EDA(c.g.c)
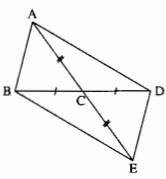
Tìm các tam giác bằng nhau trên hình bên.Giải ra nha các bạn!!

Tìm các tam giác bằng nhau trên hình bên.

Ai giúp mình nhanh mình tick cho
Tìm các tam giác cân trên hình dưới.

Các bạn giúp mk bài này với nhé:
Cho hình trên, trong đó AB // HK, AH // BK. C/m: AB = HK, AH = BK.
Cho hình bên. Lần lượt chọn mỗi đường thẳng tk, mz, nj làm cát tuyến, chỉ ra các cặp góc đồng vị, so le trong, trong cùng phía có trong hình đó.
Cho hình bs 10(hai đường thẳng a, b song song với nhau và hai đường thẳng c, d song song với nhau; Dm, Cp, Bq và An tương ứng là các tia phân giác).
a) Chứng minh: An // Cp và Dm // Bq.
b) Chứng minh: An vuông góc với Bq.
Bài I.1 trang 115 sách bài tập Toán 7 Tập 1
Cho hình bs 10(hai đường thẳng a, b song song với nhau và hai đường thẳng c, d song song với nhau; Dm, Cp, Bq và An tương ứng là các tia phân giác).
a) Chứng minh: An // Cp và Dm // Bq.
b) Chứng minh: An vuông góc với Bq.
Bài 1
Tìm x ∈ Z để B có giá trị nguyên.
Tính độ dài các đoạn thẳng AB, BC, CD và DA trên hình dưới:
Mn giải cụ thể giúp mk vs! Mơn trc!