Chọn C.
Theo giả thiết phương trình nhận z = 1+ i làm một nghiệm của phương trình: z2 + bz + c = 0.
Nên ( 1 + i) 2 + b(1 + i) + c = 0
Hay b + c + ( 2 + b) i = 0
Do đó: b + c = 0 và 2 + b = 0
Ta tìm được : b = -2 và c = 2.
Tìm các số thực a,b,c để phương trình (ẩn z) z 3 + a z 2 + b z + c = 0 nhận z = 1 + i và z = 2 làm nghiệm
Giá trị của các số thực b, c để phương trình z 2 + b z + c = 0 nhận số phức z = 1 + i làm một nghiệm là:
A. b = 2 c = - 2
B. b = - 2 c = - 2
C. b = - 2 c = 2
D. b = 2 c = 2
Giá trị của các số thực b ; c để phương trình z2 + bz + c = 0 nhận số phức z =1 + i làm một nghiệm là:
A.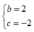 
B.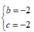 
C.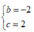 
D.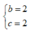 
Cho phương trình z 3 + a z 2 + b z + c = 0 nhận z = 2 và z = 1 + i làm các nghiệm của phương trình. Khi đó a - b + c là
Tìm hai số thực b và c biết rằng phương trình z 2 + b z + c = 0 có nghiệm phức z = 1+i
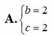
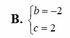
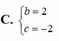
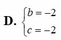
Phương trình z 2 + b z + c = 0 có một nghiệm phức là z = 1 - 2 i .Tích của hai số b và c bằng
A. 3
B.-10
C.-2 và 5
D. 5
Biết rằng phương trình z 2 + b z + c = 0 , b , c ∈ R có một nghiệm phức là z 1 = 1 + 2 i .
Khi đó b+c ?
A. b+c = 2
B. b+c = 3
C. b+c = 0
D. b+c = 7
Cho phương trình \(az^2+bz+c=0\) với a,b,c ∈ R , a ≠ 0 có các nghiệm z1,z2 đều không là số thực . Tính P |z1 +z2|2 + |z1 -z2|2 theo a,b,c
A: P= \(\dfrac{b^2-2ac}{a^2}\)
B: P= \(\dfrac{2c}{a}\)
C: P=\(\dfrac{4c}{a}\)
D: P= \(\dfrac{2b^2-4ac}{a^2}\)
Cho a,b,c là các số thực sao cho phương trình z 3 + a z 2 + b z + c = 0 có ba nghiệm phức lần lượt là z 1 = w + 3 i ; z 2 = w + 9 i ; z 3 = 2 w - 4 trong đó w là một số phức nào đó. Tính giá trị của P = a + b + c
