Các câu hỏi tương tự
Baif1: Rút gọn
A= (2x-1)^2 +2(2x-1) (2x+1) +(2x+1)^2
B=(x+y+z)^2- 2(x+2) y-y^2
Bài 2: tìm x, biết
a) (x-1) (x+1) - (x+1)^2 = 4
b) 4(x+1)^2+ (2x-1)^2 -8(x-1)(x+1)=11
c) m^2 + 6k +8 = 0
Bài 3: Tính giá trị biểu thức
a) x^2 + y^2 -5x+5y-2xy+10. Biết x-y=5
Bài 4: Cho 2(a^2+b^2) = (a+b)^2
CMR: a=b
Bài 1. Tìm giá trị nhỏ nhất của các đa thức sau:
a)A=x^2+2x+y^2+1
b)A=x^2+2xy+y^2+
Bài 2: Tìm Min của các biểu thức sau:
a)A=-3/(x^2-5x+1) b) A=6/(-x^2+2x-3)
c)A=2/(x^2+8) d)A=2/(x^2+x+4)
e)A=3y^2/(-25x^2+20xy-5y^2) (x khác 0)
f)A= y^2/(9x^2-12xy+5y^2) (x khác 0)
1.Thực hiện phép tính:
a. 3y^2*(2y-1)+y-y*(1-y+y^2)+y^2+y
b. -a^2*(3a-5)+4a*(a^2-2)
c. (4n^2-6m*n+9m^2)*(2n+3m)
d. (1+x+x^2)*(1-x)*(1+x)*(1-x+x^2)
2.Chứng minh
a. (a^2+a^2)^2-2a^2*b^2=a^4+b^4
b. (a^2+b^2)*[(a^2+b^2)^2-3a^2.b^2]=a^6+b^6
1) Làm tính nhân: a) (3-2*x+4*x^2)*(1+x-2*x^2). b) (a^2+a*x+x^2)*(a^2-a*x+x^2)*(a-x). 2) Cho đa thức: A=19*x^2-11*x^3+9-20*x+2*x^4. B=1+x^2-4*x Tìm đa thức Q và R sao cho A=B*Q+R. 3) Dùng hằng đẳng thức để làm phép chia: a) (4*x^4+12*x^2*y^2+9*y^4):(2*x^2+3*y^2). b) ( 64*a^2*b^2-49*m^4*n^2):(8*a*b+7*m^2*n). c) (27*x^3-8*y^6):(3*x-2*y^2)
1)Phân tích thành nhân tử:a. (((x^2)+(y^2))^2)((y^2)-(x^2))+(((y^2)+(z^2))^2)((z^2)-(y^2))+(((z^2)+(x^2))^2)((x^2)-(z^2))b. ((x-a)^4)+4a^4c. (x^4)-(8x^2)+4d. (x^8)+(x^4)+1e. x((y^2)-(z^2))+y((z^2)-(x^2))+z((x^2)-(y^2))f. (8x^3)(y+z)-(y^3)(z+2x)-(z^3)(2x-y)g. (12x-1)(6x-1)(4x-1)(3x-1)-52) Cho (a^3)+(b^3)+(c^3)3abc và abc khác 0. Tính A(1+a/b)(1+b/c)(1+c/a).3) Rút gọn phân thức:((x^3)+(y^3)+(z^3)-3xyz)/(((x-y)^2)+((y-z)^2)+((z-x)^2))
Đọc tiếp
1)Phân tích thành nhân tử:
a. (((x^2)+(y^2))^2)((y^2)-(x^2))+(((y^2)+(z^2))^2)((z^2)-(y^2))+(((z^2)+(x^2))^2)((x^2)-(z^2))
b. ((x-a)^4)+4a^4
c. (x^4)-(8x^2)+4
d. (x^8)+(x^4)+1
e. x((y^2)-(z^2))+y((z^2)-(x^2))+z((x^2)-(y^2))
f. (8x^3)(y+z)-(y^3)(z+2x)-(z^3)(2x-y)
g. (12x-1)(6x-1)(4x-1)(3x-1)-5
2) Cho (a^3)+(b^3)+(c^3)=3abc và abc khác 0. Tính A=(1+a/b)(1+b/c)(1+c/a).
3) Rút gọn phân thức:
((x^3)+(y^3)+(z^3)-3xyz)/(((x-y)^2)+((y-z)^2)+((z-x)^2))
Giúp mình với !
Bài 1: Phân tích các đa thức sau thành nhân tử bằng phương pháp dùng hằng đẳng thức
a, 9(a-b)^2-4(x-y)^2
b, (a^2+9)^2-36a^2
c, (x+y)^2-2(x+y)+1
d, (x-y)(x^2-z^2)-(x-z)(x^2-y^2)
Bài 2: Tìm x, biết
a, x^2+16=8x
b, 10x-x^2=25
1)cho Q=\(\dfrac{a^4+a^3-a^2-2a-2}{a^4+2a^3-a^2-4a-2}\)
Tìm GTNN của Q
2)cho \(\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1\) và \(\dfrac{a}{x}+\dfrac{b}{y}+\dfrac{c}{z}=0\)
CMR: \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}=1\)
1/ Tính giá trị nhỏ nhất (hoặc lớn nhất) của các biểu thức sau:
a, C= 3x^2 - 4x/ 1 + x^2 với mọi x.
b, D= x^2 + y^2 - x + 6y + 10 với mọi x, y.
2/ Tìm các số x và y, biết: x^3 + y^3 = 152; x^2 - xy = 19 và x - y = 2
3/ Cho x + y = 2; x^2 + y^2 = 20. Tính x^3 + y^3
4/ Cho a^2 + b^2 = 1. Chứng minh rằng: a^6 + 3.a^2.b^2 + b^6 = 1
Phân tích thành nhân tử:
a) x^2 - y^2 - 4(x-ay) - 4(a^2 - 1)
b) (x+y)^3 -1 - 3xy(x+y-1)
c) a^5 + a^4 + a^3 + a^2 + a + 1
d) 5x^3 -3x^2y - 45y^2 + 27y^3
Rút gọn biểu thức :
a,x(x+4)(x-4)-(x^2+1)(x^2-1)
b,(y-3)(y+3)(y^2+9)-(y^2+2)(y^2-2)
c,(a+b-c)^2-(a-c)^2-2ab+2ab
d,(a+b+c)^2+(b+c-a)^2)+(c+a-b)^2+(a+b-c)^2
Các bạn làm đầy đủ hộ mình nhé. Cảm ơn các bạn!




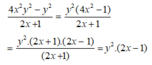
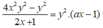 nên a = 2
nên a = 2









