Đáp án C
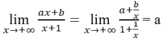
=> y = a là tiệm cận ngang.
Dựa vào đồ thị hàm số có đường thẳng y = -2 là đường tiệm cận ngang nên a = -2
Mà đồ thị hàm số đi qua điểm (0; 1) nên b = 1
Đáp án C
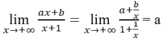
=> y = a là tiệm cận ngang.
Dựa vào đồ thị hàm số có đường thẳng y = -2 là đường tiệm cận ngang nên a = -2
Mà đồ thị hàm số đi qua điểm (0; 1) nên b = 1
Cho hàm số y = (a-1) x 4 + ( b + 2 ) x 2 + c - 1 có đồ thị như hình vẽ bên
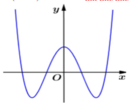
Mệnh đề nào dưới đây là đúng?
A. a > 1, b > -2, c > 1
B. a > 1, b < -2, c > 1
C. a < 1, b > -2, c > 1
D. a > 1, b < 2 , c > 1
Cho a > 0 , b > 0 , a ≠ 1 , b ≠ 1 . Đồ thị hàm số y = a x và y = log b x được xác định như hình vẽ bên. Mệnh đề nào sau đây là đúng?
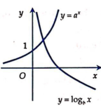
A. a > 1 ; 0 < b < 1.
B. 0 < a < 1 ; b > 1.
C. 0 < a < 1 ; 0 < b < 1.
D. a > 1 ; b > 1.
Cho hàm số y = x - a b x + c có đồ thị như hình vẽ bên. Tính giá trị của biểu thức A= a+ b+ c
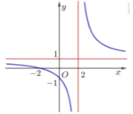
A. - 2
B. -3
C. - 4
D. -5
Xác định các hệ số a, b, c để đồ thị hàm số y = a x - 1 b x + c có đồ thị hàm số như hình vẽ bên:
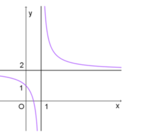
![]()
![]()
![]()
![]()
Xác định các hệ số a, b, c để đồ thị hàm số y= ax - 1 bx + c có đồ thị hàm số như hình vẽ bên:
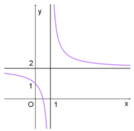
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số y= f(x) xác định và liên tục trên [ a; e] và có đồ thị hàm số y= f’ (x) như hình vẽ bên. Biết rằng f(a) + f( c)) = f( b) + f( d) . Tìm giá trị lớn nhất và nhỏ nhất của hàm số y= f( x) trên [ a; e]?
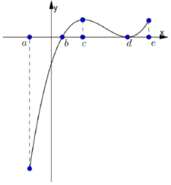
A. m a x [ a , e ] f ( x ) = f ( c ) m i n [ a , e ] f ( x ) = f ( a )
B. m a x [ a , e ] f ( x ) = f ( a ) m i n [ a , e ] f ( x ) = f ( b )
C. m a x [ a , e ] f ( x ) = f ( e ) m i n [ a , e ] f ( x ) = f ( b )
D. m a x [ a , e ] f ( x ) = f ( d ) m i n [ a , e ] f ( x ) = f ( b )
Cho hàm số f ( x ) = a x 4 + b x 2 - 1 ( a , b ∈ ℝ ) . Đồ thị của hàm số y=f(x) như hình vẽ bên. Số nghiệm thực của phương trình 2018.f(x) + 2019 = 0 là:
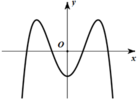
A. 4
B. 0
C. 3
D. 2
Cho 3 số a, b, c > 0, a ≠ 1 ; b ≠ 1 ; c ≠ 1 . Đồ thị các hàm số y = a x , y = b x , y = c x được cho trong hình vẽ bên dưới. Mệnh đề nào sau đây đúng?
![]()
![]()
![]()
Cho hàm số y=f(x) có đồ thị như hình vẽ và diện tích hai phần A, B lần lượt bằng 12 và 2. Giá trị của I = ∫ - 1 - 2 5 f ( 5 x + 3 ) d x bằng
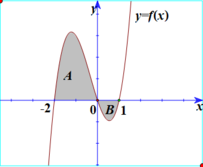
A. 50.
B. 14 5 .
C. 14.
D. 2 .