A=2003x(1+x+x2+...+x98+x99)
=> \(\frac{A}{2003x}=1+x+x^2+...+x^{98}+x^{99}\)
=> \(\frac{A.x}{2003x}=x+x^2+...+x^{98}+x^{99}+x^{100}\)=> \(\frac{A}{2003}=x+x^2+...+x^{98}+x^{99}+x^{100}\)
=> \(\frac{A}{2003}-\frac{A}{2003x}=\left(x+x^2+...+x^{98}+x^{99}+x^{100}\right)-\left(1+x+x^2+...+x^{98}+x^{99}\right)\)
=> \(\frac{A\left(x-1\right)}{2003x}=x^{100}-1\)=> \(A=\frac{2003x\left(x^{100}-1\right)}{x-1}\)
Thay x=2004 ta được: \(A=\frac{2003.2004\left(2004^{100}-1\right)}{2004-1}=2004\left(2004^{100}-1\right)\)
Đáp số: \(A=2004\left(2004^{100}-1\right)\)












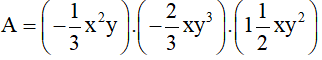
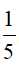 ; y = -1
; y = -1