Các câu hỏi tương tự
Hình hộp chữ nhật ABCD.A’B’C’D’ có AC a
3
, AD 2a, AB a
5
. Tính thể tích V của hình hộp. A. V
2
a
3
15
B. V
a
3
15
3
C. V
a
3
6
D. V
3
a...
Đọc tiếp
Hình hộp chữ nhật ABCD.A’B’C’D’ có AC = a 3 , AD' = 2a, AB' = a 5 . Tính thể tích V của hình hộp.
A. V = 2 a 3 15
B. V = a 3 15 3
C. V = a 3 6
D. V = 3 a 3
Tính thể tích V của khối hộp chữ nhật ABCD.ABCD biết ABa, AD2a, ACa
14
.
Đọc tiếp
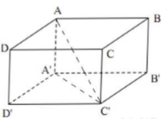
Tính thể tích V của khối hộp chữ nhật ABCD.A'B'C'D' biết AB=a, AD=2a, AC'=a 14 .
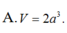
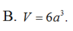
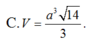
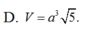
Cho hình chóp S.ABC đáy ABC là tam giác vuông tại C, có cạnh AB a = , cạnh bên SA vuông góc mặt phẳng đáy và SA a = 3 . Tính thể tích V khối cầu ngoại tiếp hình chóp.
A. V= 2 2 3 3 a .
B. V= 3 4a .
C. V= 32 3 3 πa .
D. V= 4 3 3 πa .
Cho hình hộp chữ nhật
A
B
C
D
.
A
B
C
D
có
A
B
a
,
A
D
2
a
,
A
C
2
3
a
. Tính theo a thể tích V của khối hộp ABCD.A’B’C’D’. A.
V
2
6
a
3
B...
Đọc tiếp
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có A B = a , A D = 2 a , A C ' = 2 3 a . Tính theo a thể tích V của khối hộp ABCD.A’B’C’D’.
A. V = 2 6 a 3
B. V = 2 6 3 a 3
C. V = 3 2 a 3
D. V = 6 a 3
Một hình hộp chữ nhật có ba kích thước là
a
,
b
,
c
. Thể tích
V
của khối hộp chữ nhật đó bằng A.
a
+
c
b
B.
a
b
c
C.
a
+
b
c
D.
1
3
a...
Đọc tiếp
Một hình hộp chữ nhật có ba kích thước là a , b , c . Thể tích V của khối hộp chữ nhật đó bằng
A. a + c b
B. a b c
C. a + b c
D. 1 3 a b c
Cho hình chóp tam giác đều S.ABCD, cạnh đáy bằng a. Mặt bên tạo với mặt đáy một góc 60. Tính thể tích V của hình chóp S.ABCD. A)a³✓3/2 B)a³✓3/6 C)a³✓3/12 D)a³✓3/24
Một hình hộp chữ nhật có kích thước
a
(
c
m
)
x
b
(
c
m
)
x
c
(
c
m
)
trong đó a, b, c là các số nguyên và
1
≤
a
≤
b
≤
c
. Gọi
v
(
c
m
3
)
và
s
(
c
m
2...
Đọc tiếp
Một hình hộp chữ nhật có kích thước a ( c m ) x b ( c m ) x c ( c m ) trong đó a, b, c là các số nguyên và 1 ≤ a ≤ b ≤ c . Gọi v ( c m 3 ) và s ( c m 2 ) lần lượt là thể tích và diện tích toàn phần của hình hộp. Biết V = s tìm số các bộ ba số ( a , b , c ) .
A. 4
B. 10
C. 12
D. 21
Cho hình chóp tứ giác S.ABCD có thể tích bằng V. Lấy điểm A' trên cạnh SA sao cho SA' = SA/3. Mặt phẳng qua A' và song song với đáy của hình chóp cắt cạnh SB, SC, SD lần lượt tại B', C', D'. Thể tích hình chóp S.A'B'C'D' bằng:
A. V/3 B. V/9
C. V/27 D. V/81.
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, AA’ = c. Gọi M và N theo thứ tự là trung điểm của A’B’ và B’C’. Tính tỉ số giữa thể tích khối chóp D’.DMN và thể tích khối hộp chữ nhật ABCD.A’B’C’D’