Chọn D.
Giả thiết khoảng cách giữa một đường thẳng bất kỳ của đáy này tới một đường thẳng bất kỳ của đáy kia bằng h cho ta thông tin chiều cao của lăng trụ bằng h vì 2 đáy song song với nhau. Do đó V = B.h
Thể tích V của một khối lăng trụ có diện tích đáy bằng B và chiều cao bằng h là
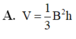
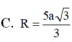
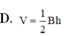
Thể tích V của khối lăng trụ có chiều cao bằng h và diện tích đáy bằng B là
Thể tích V của khối lăng trụ có chiều cao bằng h và diện tích đáy bằng B là:
A. V = Bh
B. V = 1 2 Bh
C. V = 1 6 Bh
D. V = 1 3 Bh
Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác vuông tại B, A B = a , B C = 2 a . Hình chiếu vuông góc của A’ trên đáy ABC là trung điểm H của cạnh AC, đường thẳng A’B tạo với đáy một góc 45 0 . Tính thể tích V của khối lăng trụ ABC.A’B’C’
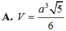
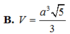
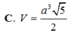
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh 2a, biết thể tích của khối lăng trụ ABC.A'B'C' bằng a 3 . Tính khoảng cách h giữa hai đường thẳng AB và B'C'.
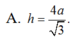
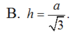
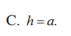
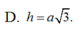
Cho khối lăng trụ có diện tích đáy bằng a2 và khoảng cách giữa hai đáy bằng 3a. Tính thể tích V của khối lăng trụ đã cho.
A. V = 3 2 a 3
B. V=3a3
C. V=a3
D. V=9a3.
Thế tích V của khối lăng trụ có chiều cao bằng h và diện tích đáy bằng B được tính theo công thức nào dưới đây?
A. V= 1 3 Bh
B. V=3Bh
C. V=Bh
D. V= 1 2 Bh
Thể tích của khối lăng trụ có diện tích đáy bằng Hàm số đồng biến trên khoảng B và chiều cao bằng h là
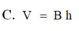
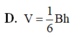
Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A' lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Biết khoảng cách giữa hai đường thẳng AA' và BC bằng a√3/4. Tính thể tích V của khối lăng trụ ABC.A'B'C'
A. V = a 3 3 6
B. V = a 3 3 3
C. V = a 3 3 24
D. V = a 3 3 12
