Điều kiện xác định của hàm số: x - 1 ≥ 0 3 - x ≥ 0 ⇔ x ≥ 1 x ≤ 3 ⇔ 1 ≤ x ≤ 3
Tập xác định của hàm số là: D= [1; 3]
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Câu 1.
a) Cho tập A,B lần lượt là tập xác định của hàm số f(x) = \(\sqrt{6-x}\) và g(x) = \(\dfrac{3}{2x+1}\). Xác định các tập A∩B, A∪B, A∖B, CRA.
b) Cho tập hợp C=[−3;8] và D=[m−6;m+3). Với giá trị nào của m thì C∩D là một đoạn thẳng có độ dài bằng 4.
Tìm tập xác định D của hàm số
y
x
+
2
-
x
+
3
A. B. C. D R. D.
Đọc tiếp
Tìm tập xác định D của hàm số y = x + 2 - x + 3
A. 
B. 
C. D = R.
D. 
Tìm tập xác định D của hàm số
y
x
+
2
−
x
+
3
A. D
[
−
3
;
+
∞
)
B. D
[
−
2
;
+
∞
)
C. D R D. D
[
2
;
+
∞
)
Đọc tiếp
Tìm tập xác định D của hàm số y = x + 2 − x + 3
A. D = [ − 3 ; + ∞ )
B. D = [ − 2 ; + ∞ )
C. D = R
D. D = [ 2 ; + ∞ )
I. HÀM SỐ, TXĐ, CHẴN LẺ, ĐƠN ĐIỆU, ĐỒ THỊ.1. TXĐ CỦA HÀM SỐCâu 1.Tìm tập xác định của hàm số ydfrac{sqrt{x-1}}{x-3}Câu 2.Tìm tập xác định của hàm số y sqrt[3]{x-1}Câu 3. Tìm tập xác định của hàm số ydfrac{sqrt[3]{1-x}+3}{sqrt{x+3}}Câu 4. Tìm tập xác định của hàm số ysqrt{left|x-2right|}
Đọc tiếp
I. HÀM SỐ, TXĐ, CHẴN LẺ, ĐƠN ĐIỆU, ĐỒ THỊ.
1. TXĐ CỦA HÀM SỐ
Câu 1.Tìm tập xác định của hàm số y=\(\dfrac{\sqrt{x-1}}{x-3}\)
Câu 2.Tìm tập xác định của hàm số y= \(\sqrt[3]{x-1}\)
Câu 3. Tìm tập xác định của hàm số y=\(\dfrac{\sqrt[3]{1-x}+3}{\sqrt{x+3}}\)
Câu 4. Tìm tập xác định của hàm số y=\(\sqrt{\left|x-2\right|}\)
Tìm tập xác định của hàm số
y
x
2
+
x
-
2
x
2
-
1
A. x -2; x ≤ -2; B. x ≤ -2; x ≥ -1 C. x ≤ -2; x ≤ -2; D. x ≤ -2; -1 x 1; x 1
Đọc tiếp
Tìm tập xác định của hàm số y = x 2 + x - 2 x 2 - 1
A. x < -2; x ≤ -2;
B. x ≤ -2; x ≥ -1
C. x ≤ -2; x ≤ -2;
D. x ≤ -2; -1 < x < 1; x > 1
Đồ thị hàm số
y
f
(
x
)
x
2
-
4
x
+
3
được cho trong hình 46. Từ hình vẽ nãy hãy chỉ ra tập nghiệm của bất phương trình
x
2
-
4
x
+
3
...
Đọc tiếp
Đồ thị hàm số y = f ( x ) = x 2 - 4 x + 3 được cho trong hình 46. Từ hình vẽ nãy hãy chỉ ra tập nghiệm của bất phương trình x 2 - 4 x + 3 > 0
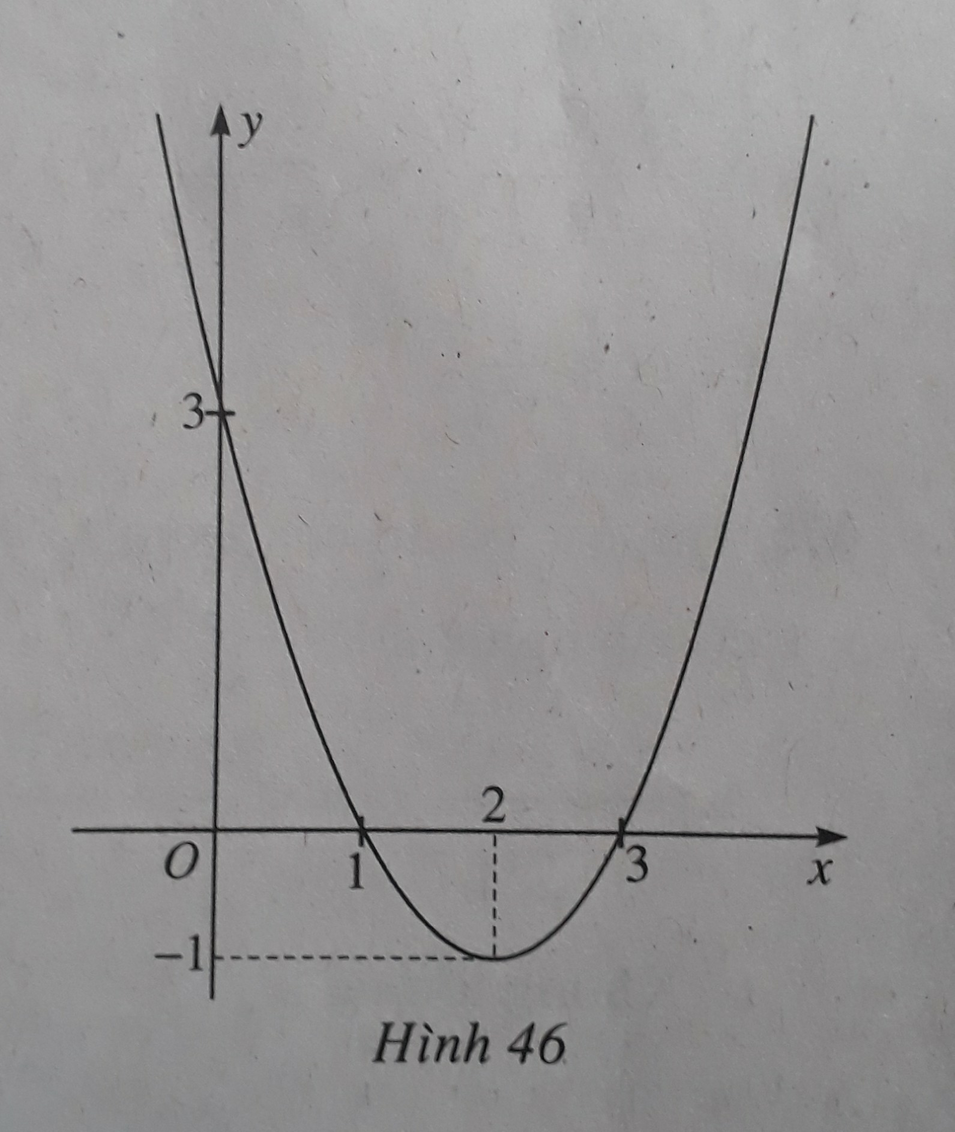
A. x < 1
B. x ≥ 1
C. 1 < x < 3
D. ( - ∞ ; 1 ) ∪ ( 3 ; + ∞ )
tập xác định d của hàm số y=3x-1/x+1
tập xác định d của hàm số y=3x-1/x+1
Hàm số \(\dfrac{x+2}{x-m+2}\) xác định trên (1; 3) khi:
A. m < 3 B. m ≥5 C. m < 3 hoặc m > 5 D. m ≥ 5 hoặc m ≤ 3.
Tập xác định D của hàm số
y
2
x
-
1
2
x
+
1
x
-
3
là: A. B. C. D. D R.
Đọc tiếp
Tập xác định D của hàm số y = 2 x - 1 2 x + 1 x - 3 là:
A. 
B. 
C. 
D. D = R.