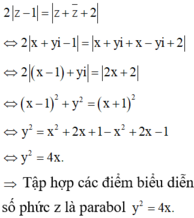Các câu hỏi tương tự
Tập hợp các điểm biểu diễn số phức z thỏa mãn 2|z-1| = |z + z ¯ +2| trên mặt phẳng tọa độ là một
A. đường thẳng.
B. đường tròn.
C. parabol.
D. hypebol.
Tập hợp các điểm biểu diễn số phức z thỏa mãn 2|z-1| = |z + z ¯ + 2| trên mặt phẳng tọa độ là một
A. đường thẳng
B. đường tròn
C. parabol
D. hypebol
Tập hợp các điểm biểu diễn số phức z thỏa mãn |z + 2| + |z – 2| = 5 trên mặt phẳng tọa độ là một
A. đường thẳng.
B. đường tròn.
C. elip.
D. hypebol.
Cho số phức z thỏa mãn: |z - 1 + i| = 2. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức z là:
A. Một đường thẳng.
B. Một đường Parabol.
C. Một đường tròn có bán kính bằng 2.
D. Một đường tròn có bán kính bằng 4.
Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn số phức z thỏa mãn
1
≤
z
≤
2
là một hình phẳng tích bằng
Đọc tiếp
Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn số phức z thỏa mãn 1 ≤ z ≤ 2 là một hình phẳng tích bằng
![]()
![]()
![]()
![]()
Tập hợp các điểm biểu diễn số phức z thỏa mãn | z | < 1 trên mặt phẳng tọa độ là:
A. Hình tròn tâm O, bán kính R = 1, không kể biên.
B. Hình tròn tâm O, bán kính R = 1, kể cả biên.
C. Đường tròn tâm O, bán kính R = 1.
D. Đường tròn tâm bất kì, bán kính R = 1.
Cho các số phức z thỏa mãn
z
−
i
z
−
1
+
2
i
. Tập hợp các điểm biểu diễn số phức
w
2
−
i
z
+
1
trên mặt phẳng tọa độ là một đường thẳng. Phương trình đường thẳng đó là A....
Đọc tiếp
Cho các số phức z thỏa mãn z − i = z − 1 + 2 i . Tập hợp các điểm biểu diễn số phức w = 2 − i z + 1 trên mặt phẳng tọa độ là một đường thẳng. Phương trình đường thẳng đó là
A. x − 7 y − 9 = 0
B. x + 7 y − 9 = 0
C. x + 7 y + 9 = 0
D. x - 7 y + 9 = 0
Tìm tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ thỏa mãn các điều kiện: |2 + z| < |2 – z|
Cho số phức z thay đổi hoàn toàn thỏa mãn: |z-i| = |z-1+2i|. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức w thỏa mãn: w = (2-i)z+1 là một đường thẳng. Viết phương trình đường thẳng đó.
A. -x + 7y + 9 = 0
B. x + 7y - 9 = 0
C. x + 7y + 9 = 0
D. x - 7y + 9 = 0