Các câu hỏi tương tự
Trong tất cả các giá trị của tham số mm để hàm số y=\dfrac{1}{3} x^{3} +mx^{2} -mx-my=31x3+mx2−mx−m đồng biến trên \mathbb{R},R, giá trị nhỏ nhất của mm là
Tập tất cả các giá trị của tham số m để hàm số y ln(cosx + 2) – mx + 1 đồng biến trên R là A.
(
-
∞
;
-
1
3
]
B.
(
-
∞
;
-
1
3
]
C.
[
-
1
3
;
+
∞
)
D.
[
-...
Đọc tiếp
Tập tất cả các giá trị của tham số m để hàm số y = ln(cosx + 2) – mx + 1 đồng biến trên R là
A. ( - ∞ ; - 1 3 ]
B. ( - ∞ ; - 1 3 ]
C. [ - 1 3 ; + ∞ )
D. [ - 1 3 ; + ∞ )
Cho X là tập hợp tất cả các giá trị nguyên thuộc đoạn
[
-
5
;
5
]
của tham số m để hàm số
y
x
3
-
3
x
2
+
m
x
-
2
đồng biến trên khoảng
2
;
+
∞
. Số phần tử của X là A. 3 B. 6 C. 2 D. 5
Đọc tiếp
Cho X là tập hợp tất cả các giá trị nguyên thuộc đoạn [ - 5 ; 5 ] của tham số m để hàm số y = x 3 - 3 x 2 + m x - 2 đồng biến trên khoảng 2 ; + ∞ .
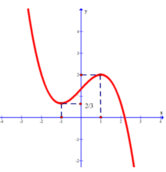
Số phần tử của X là
A. 3
B. 6
C. 2
D. 5
Cho hàm số \(f\left(x\right)=\frac{1}{5}m^2x^5-\frac{1}{3}mx^3+10x^2-\left(m^2-m-20\right)x\)Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số đồng biến trên R. Tổng giá trị của tất cả các phần tử thuộc S bằng :
A. 3/2
B. -2
C. 5/2
D. 1/2
Tìm tất cả giá trị thực của tham số m để hàm số
y
x
3
3
+
(
m
+
1
)
x
2
+
(
3
m
+
1
)
x
+
2
đồng biến trên R A. B. C. D.
Đọc tiếp
Tìm tất cả giá trị thực của tham số m để hàm số y = x 3 3 + ( m + 1 ) x 2 + ( 3 m + 1 ) x + 2 đồng biến trên R
A.![]()
B.![]()
C. ![]()
D. ![]()
Tìm tất cả các giá trị thực của tham số m để hàm số y(m-3)x-(2m+1)cosx nghịch biến trên R. A. B. không có m C. D.
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y=(m-3)x-(2m+1)cosx nghịch biến trên R.
A.![]()
B. không có m
C. ![]()
D. ![]()
Tìm tất cả các giá trị của tham số m để hàm số
y
1
3
x
3
+
(
m
-
1
)
x
2
+
(
2
m
-...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để hàm số y = 1 3 x 3 + ( m - 1 ) x 2 + ( 2 m - 3 ) x - 2 3 đồng biến trên
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]()
Tập hợp S tất cả các giá trị của tham số thực m để hàm số: y
1
3
x
3
-
(
m
+
1
)
x
2
+
(
m
2
+
2
m
)
x
-
3
nghịch biến trên khoảng (-1;1) là A. S
∅...
Đọc tiếp
Tập hợp S tất cả các giá trị của tham số thực m để hàm số: y = 1 3 x 3 - ( m + 1 ) x 2 + ( m 2 + 2 m ) x - 3 nghịch biến trên khoảng (-1;1) là
A. S = ∅
B. S = [0;1]
C. S = [-1;0]
D. S = {-1}
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
3
+
2
(
m
-
1
)
x
2
+
(
m
-
1
)
x
+
5
đồng biến trên
ℝ
A.
m
∈
(
-
∞
;
1
]
B. ...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 + 2 ( m - 1 ) x 2 + ( m - 1 ) x + 5 đồng biến trên ℝ
A. m ∈ ( - ∞ ; 1 ]
B. m ∈ 1 ; 7 4
C. m ∈ - ∞ ; 1 ∪ 7 4 ; + ∞
D. m ∈ 1 ; 7 4