Các câu hỏi tương tự
Tam giác ABC có I là giao điểm các tia phân giác của các góc B và C. Gọi d là giao điểm của AI và BC. Kẻ IH vuông góc với BC( H thuộc BC). Chứng minh rằng góc BIH= góc CID.
Tam giác ABC có I là giao điểm các tia phân giác của các góc B và C. Gọi D là giao điểm AI và BC. Kẻ IH vuông góc với BC( H thuộc BC). Chứng minh BIH bằng CID
1)Tam giác ABC vuông cân tại A, đường trung tuyến AM. Gọi D là điểm thuộc đoạn thẳng MC. Gọi H là chân đường vuông góc kẻ từ B đến AD. Gọi I, K lần lượt là chân đường vuông góc kẻ từ M đến AD và BH. Chứng minh HM là tia phân giác của góc BHD.2)Tam giác ABC có I là giao điểm các tia phân giác của các góc B và C. Gọi d là giao điểm của AI và BC. Kẻ IH vuông góc với BC( H thuộc BC). Chứng minh rằng góc BIH góc CID.3) Cho tam giác ABC có góc C30 độ. Tia phân giác của góc B và đường phân giác của góc...
Đọc tiếp
1)Tam giác ABC vuông cân tại A, đường trung tuyến AM. Gọi D là điểm thuộc đoạn thẳng MC. Gọi H là chân đường vuông góc kẻ từ B đến AD. Gọi I, K lần lượt là chân đường vuông góc kẻ từ M đến AD và BH. Chứng minh HM là tia phân giác của góc BHD.
2)Tam giác ABC có I là giao điểm các tia phân giác của các góc B và C. Gọi d là giao điểm của AI và BC. Kẻ IH vuông góc với BC( H thuộc BC). Chứng minh rằng góc BIH= góc CID.
3) Cho tam giác ABC có góc C=30 độ. Tia phân giác của góc B và đường phân giác của góc ngoài tại A cắt nhau ở E. Tính số đo góc BCE.
B1: Cho tam giác ABC có góc C bằng 30 độ. Tia phân giác của góc B và đường phân giác góc ngoài tại A cắt nhau ở E. Tính số đo góc BCEB2: Cho tam giác ABC có I là giao điểm các tia pg của góc B và góc C. Gọi D là giao điểm của AI và BC. Kẻ IH vuông góc BC (H thuộc BC) CMR: góc BIH góc CIDB3: Cho tam giác ABC vuông tại A. Kẻ AH vuông góc BC. (H thuộc BC), các tia pg của góc HAC và AHC cắt nhau ở I. Tia phân giác của góc HAB cắt BC ở D. Cm: CI điq ua trung điểm của AD
Đọc tiếp
B1: Cho tam giác ABC có góc C bằng 30 độ. Tia phân giác của góc B và đường phân giác góc ngoài tại A cắt nhau ở E. Tính số đo góc BCE
B2: Cho tam giác ABC có I là giao điểm các tia pg của góc B và góc C. Gọi D là giao điểm của AI và BC. Kẻ IH vuông góc BC (H thuộc BC) CMR: góc BIH = góc CID
B3: Cho tam giác ABC vuông tại A. Kẻ AH vuông góc BC. (H thuộc BC), các tia pg của góc HAC và AHC cắt nhau ở I. Tia phân giác của góc HAB cắt BC ở D. Cm: CI điq ua trung điểm của AD
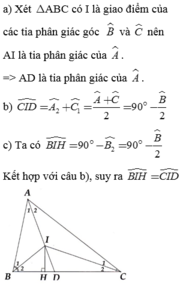
Cho tam giác ABC , I là giao điểm các tia phân giác của góc B và C.Gọi D là giao điểm AI và BC .Kẻ IH vuông góc với BC ( H thuộc BC)
C/m góc BIH = góc CID
tam giác abc có I là giao điểm các tia phân giác của các góc B và C gọi D là giao điểm của ai và Bc kẻ ih vuông với bc cm bih = cid
tam giác ABC có I là giáo điểm của các tia phân giác góc B , C . gọi D là giao điểm của AI, BC ,Kẻ IH vuông với BC .CM góc BIH = góc CID
1. Cho tam giác abc. Các tia phân giác của các góc b và c cắt nhau tại i. Qua i kẻ đường thẳng song song vói ab, cắt ac và bc ở d và e. CMR: de ad + be2. Cho tam giác abc vuông tại a. Các tia phân giác của các góc b và c cát nhau tại i. Kẻ ih vuông góc với bc(h thuộc bc). Biết hi a; hb 2a; hc 3a. Tính chu vi tam giác abc.3. Tm giác abc có i là giao điểm các tia phân giác của các góc b và c. Gọi d là giao điểm của ai và bc. Kẻ ih vuông góc với bc(h thuộc bc). CMR: góc bih góc cid.4.Cho tam...
Đọc tiếp
1. Cho tam giác abc. Các tia phân giác của các góc b và c cắt nhau tại i. Qua i kẻ đường thẳng song song vói ab, cắt ac và bc ở d và e. CMR: de = ad + be
2. Cho tam giác abc vuông tại a. Các tia phân giác của các góc b và c cát nhau tại i. Kẻ ih vuông góc với bc(h thuộc bc). Biết hi = a; hb = 2a; hc = 3a. Tính chu vi tam giác abc.
3. Tm giác abc có i là giao điểm các tia phân giác của các góc b và c. Gọi d là giao điểm của ai và bc. Kẻ ih vuông góc với bc(h thuộc bc). CMR: góc bih = góc cid.
4.Cho tam giác abc có góc b> góc c, đường phân giác ad. Gọi h là chân đường vuông góc kẻ từ a đến bc. CMR: góc had=góc(b-c)/2.
5. Tam giác abc có góc b lớn hơn góc c 90 độ. Các đường phân giác trong và ngoài của góc a cắt bc ở d và e. CMR:tam giác ade vuông cân.
6. Cho tam giác abc, ad là phân giác trong của góc a. CMR: bd/dc = ab/ac.
7. Cho tam giác abc, bc = a, ca = b, ab = c. Các phân giác ad, be, cf cắt nhau tại i. CMR:a) di/da = a/a+b+c
b) di/da + ei/eb + fi/fc = 1
Bài 1: Cho tam giác ABC ở phía ngoài tam giác ABC vẽ các tam giác vuông tại A là ABD và ACE có ABAD, ACAE. Kẻ AH vuông góc với BC, gọi I là giao điểm của AH với DE. Kẻ DM vuông góc với IH, EL vuông góc với IH. Chứng minh: a) Tam giác HBD tam giác MAD b) Tam giác HCA tam giác LEAc) IDIEBài 2: Cho tam giác ABC có ABAC. Trên tia đối của tia CA lấy điểm D sao cho CDAB. Gọi I là giao điểm của đường trung trực của BC và AD. Chứng minh:a) Tam giác AIB tam giác DICb) AI là tia phân giác của góc BACc) K...
Đọc tiếp
Bài 1: Cho tam giác ABC ở phía ngoài tam giác ABC vẽ các tam giác vuông tại A là ABD và ACE có AB=AD, AC=AE. Kẻ AH vuông góc với BC, gọi I là giao điểm của AH với DE. Kẻ DM vuông góc với IH, EL vuông góc với IH. Chứng minh:
a) Tam giác HBD= tam giác MAD
b) Tam giác HCA= tam giác LEA
c) ID=IE
Bài 2: Cho tam giác ABC có AB>AC. Trên tia đối của tia CA lấy điểm D sao cho CD=AB. Gọi I là giao điểm của đường trung trực của BC và AD. Chứng minh:
a) Tam giác AIB= tam giác DIC
b) AI là tia phân giác của góc BAC
c) Kẻ IE vuông góc với AB. Chứng minh AE=\(\frac{1}{2}\) AD