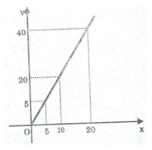
S A B C là hàm số của chiều cao AH.
Gọi y là diện tích của
△
ABC (
c
m
2
) và x là độ dài AH (cm) thì 
Đồ thị như hình bên.
Tam giác ABC có đáy BC cố định và dài 4cm. Đỉnh A di chuyển trên đường thẳng d ( d ⊥ BC). Gọi H là chân đường cao hạ từ đỉnh A đến đường thẳng BC. Diện tích tam giác tỉ lệ thuận với chiều cao AH không?
Tam giác ABC có đáy BC cố định và dài 4cm. Đỉnh A di chuyển trên đường thẳng d ( d ⊥ BC). Gọi H là chân đường cao hạ từ đỉnh A đến đường thẳng BC. Điền vào ô trống bảng sau:
| Độ dài AH (cm) | 1 | 2 | 3 | 4 | 5 | 10 | 15 | 20 |
| S A B C ( c m 2 ) |
Cho tam giác ABC có BC cố định, đỉnh A di chuyển trên đường thẳng d song song với BC và cách BC 3cm. Hỏi trọng tâm G của tam giác ABC di chuyển trên đường nào?
Cho tam giác ABC có đáy BC cố định và đỉnh A di động trên đường thẳng d cố định song song BC. Chứng minh rằng khi A di động trên d thì diện tích tam giác ABC không đổi
Cho tam giác ABC có đáy BC cố định và đỉnh A di động trên đường thẳng d cố định song song với BC. Chứng minh rằng tam giác ABC có diện tích không đổi.
Cho tam giác ABC vuông tại A, chân H của đường cao AH chia cạnh huyền BC thành hai đoạn có độ dài 4cm và 9cm.
Gọi D và E là hình chiếu của H trên AB và AC.
Các đường thẳng vuông góc với DE tại D và E cắt BC theo thứ tự tại M và N . Chứng minh M là trung điểm của BH , N là trung điểm của CH.
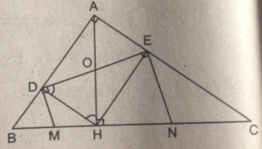
Cho tam giác ABC vuông tại A, chân H của đường cao AH chia cạnh huyền BC thành hai đoạn có độ dài 4cm và 9cm.
Gọi D và E là hình chiếu của H trên AB và AC.
Tính độ dài DE
Cho tam giác ABC có AB = 4cm, BC = 6cm BD là đường phân giác xuất phát từ đỉnh B (D thuộc AC). Gọi E, F lần lượt là hình chiếu của A và C trên đường thẳng BD.
cho hình chữ nhật ABCD có AB=4cm AD=3cm. gọi H là chân đường vuông kẻ từ A đến cạnh BD.
a, chứng minh rằng tam giác ABD đồng dạng với tam giác HAD.
b, tính độ dài đoạn thẳng BD, HD.
c, đường thẳng AH cắt DC tại I và cắt đường thẳng BC tại K. tính tỉ số diện tích của hai tam giác ABH và BKH
