Các câu hỏi tương tự
Cho lăng trụ lục giác đều Hỏi có bao nhiêu hình chóp tứ giác có 5 đỉnh là đỉnh của lăng trụ?
A. 492
B. 200
C. 360
D. 510
Trong các loại hình sau: Tứ diện đều; hình chóp tứ giác đều; hình lăng trụ tam giác đều; hình hộp chữ nhật, loại hình nào có ít mặt phẳng đối xứng nhất A. Tứ diện đều B. Hình chóp tứ giác đều C. Hình lăng trụ tam giác đều D. Hình hộp chữ nhật
Đọc tiếp
Trong các loại hình sau: Tứ diện đều; hình chóp tứ giác đều; hình lăng trụ tam giác đều; hình hộp chữ nhật, loại hình nào có ít mặt phẳng đối xứng nhất
A. Tứ diện đều
B. Hình chóp tứ giác đều
C. Hình lăng trụ tam giác đều
D. Hình hộp chữ nhật
Cho hình chóp tứ giác đều S.ABCD. Số mặt phẳng qua điểm S cách đều các điểm A, B, C, D là
A. 4
B. 2
C. 3
D. 1
Cho hình chóp tứ giác đều S.ABCD. Số mặt phẳng qua điểm S cách đều các điểm A,B,C,D là:
A. 4
B. 2
C. 3
D. 1
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Tính cosin của góc giữa một mặt bên và một mặt đáy.
A. 1 2
B. 1 3
C. 1 3
D. 1 2
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a. Mặt bên của hình chóp tạo với mặt đáy một góc
60
o
. Mặt phẳng (P) chứa AB và đi qua trọng tâm G của tam giác SAC cắt SC, SD lần lượt tại M và N. Thể tích khối chóp S.ABMN là
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a. Mặt bên của hình chóp tạo với mặt đáy một góc 60 o . Mặt phẳng (P) chứa AB và đi qua trọng tâm G của tam giác SAC cắt SC, SD lần lượt tại M và N. Thể tích khối chóp S.ABMN là
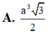
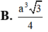
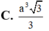
![]()
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a. Mặt bên của hình chóp tạo với mặt đáy một góc
60
o
. Mặt phẳng (P) chứa AB và đi qua trọng tâm G của tam giác SAC cắt SC, SD lần lượt tại M và N. Thể tích khối chóp S.ABMN là
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a. Mặt bên của hình chóp tạo với mặt đáy một góc 60 o . Mặt phẳng (P) chứa AB và đi qua trọng tâm G của tam giác SAC cắt SC, SD lần lượt tại M và N. Thể tích khối chóp S.ABMN là
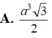
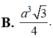
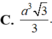
![]()
Cho hình chóp tứ giác đều S. ABCD, có cạnh đáy bằng a và có thể tích
a
3
3
6
Gọi J là điểm cách đều tất cả các mặt của hình chóp. Tính khoảng cách d từ J đến mặt phẳng đáy A.
d
a
3
4
B. ...
Đọc tiếp
Cho hình chóp tứ giác đều S. ABCD, có cạnh đáy bằng a và có thể tích a 3 3 6 Gọi J là điểm cách đều tất cả các mặt của hình chóp. Tính khoảng cách d từ J đến mặt phẳng đáy
A. d = a 3 4
B. d = a 3 2
C. d = a 3 6
D. d = a 3 3
Cho hình chóp tứ giác đều S.ABCD. Gọi H là chân đường cao của hình chóp. Một mặt phẳng (P) thay đổi cắt các cạnh bên SA, SB, SC, SD lần lượt tại E, F, I, J. Gọi K EI ∩ FJ. Đặt SE a, SF b, SI c, SJ d, SK k, ∠ASH α.a) Tìm diện tích của tam giác SEI theo a, c, αb) Chứng minh rằng
1
a
+
1
b
2
cos
α...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD. Gọi H là chân đường cao của hình chóp. Một mặt phẳng (P) thay đổi cắt các cạnh bên SA, SB, SC, SD lần lượt tại E, F, I, J. Gọi K = EI ∩ FJ. Đặt SE = a, SF = b, SI = c, SJ = d, SK = k, ∠ASH = α.
a) Tìm diện tích của tam giác SEI theo a, c, α
b) Chứng minh rằng 1 a + 1 b = 2 cos α k
Suy ra 1 a + 1 c = 1 b + 1 d
Cho hình chóp tứ giác đều S.ABCD có cạnh bên và cạnh đáy đều bằng a. Gọi O là tâm của ABCD. Gọi M là trung điểm SC và M là hình chiếu vuông góc của M lên (ABCD). Diện tích của tam giác M BD bằng: A.
a
2
6
8
B.
a
2
2
C. ...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh bên và cạnh đáy đều bằng a. Gọi O là tâm của ABCD. Gọi M là trung điểm SC và M' là hình chiếu vuông góc của M lên (ABCD). Diện tích của tam giác M' BD bằng:
A. a 2 6 8
B. a 2 2
C. 2 a 2 8
D. a 2 4



