Question

Sử dụng bài 55 để chứng minh rằng: Điểm cách đều ba đỉnh của một tam giác vuông là trung điểm của cạnh huyền của tam giác đó.

Từ đó hãy tính độ dài đường trung tuyến xuất phát từ đỉnh góc vuông theo độ dài cạnh huyền của một tam giác vuông.

Answer 1

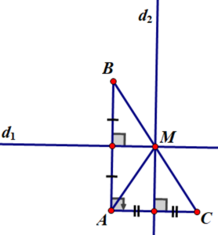
+ Giả sử ∆ABC vuông tại A.

d1 là đường trung trực cạnh AB, d2 là đường trung trực cạnh AC.

d1 cắt d2 tại M. Khi đó M là điểm cách đều ba đỉnh của tam giác ABC.

+ Áp dụng kết quả bài 55 ta có B, M, C thẳng hàng.

QUẢNG CÁO

+ M cách đều A, B, C ⇒ MB = MC ⇒ M là trung điểm của cạnh BC (đpcm)

+ M là trung điểm của cạnh BC (đpcm)

*) Giả sử AM là trung tuyến của tam giác ABC suy ra M là trung điểm của cạnh BC

⇒ MB = MC = BC/2

Mà MA = MB = MC (cmt)

⇒ MA = BC/2

Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền.