\(\dfrac{2^2}{3\cdot5}+\dfrac{2^2}{5\cdot7}+\dfrac{2^2}{7\cdot9}+...+\dfrac{2^2}{97\cdot99}\)
\(=2\dfrac{2}{3\cdot5}+2\dfrac{2}{5\cdot7}+2\dfrac{2}{7\cdot9}+...+2\dfrac{2}{97\cdot99}\)
\(=2\left(\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+\dfrac{2}{7\cdot9}+...+\dfrac{2}{97\cdot99}\right)\)
\(=2\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+...+\dfrac{1}{97}-\dfrac{1}{99}\right)\)
\(=2\left(\dfrac{1}{3}-\dfrac{1}{99}\right)\\ =2\cdot\dfrac{32}{99}\\ =\dfrac{64}{99}\)
Đúng 2
Bình luận (0)
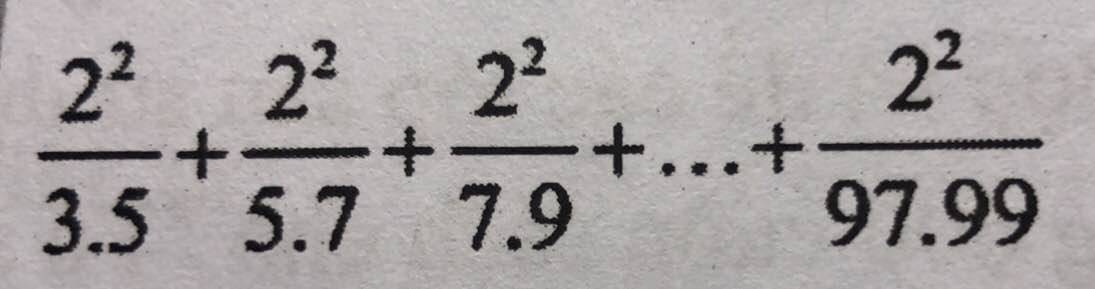
Mấy bạn giúp mik lẹ zới , cho mik đáp án đầy đủ trong vòng 10phut nha , ( các bạn làm đc bài nào thì làm ) 
