Đáp án C.
Điều kiện x > 2 ; x ≠ 4 .
Phương trình tương đương log3 (x – 2)2 + log3 (x – 4)2 = 0
<=> log3 [(x – 2)2(x – 4)2] = 0 <=> (x – 2)2(x – 4)2 = 1 <=> x = 3.
Đáp án C.
Điều kiện x > 2 ; x ≠ 4 .
Phương trình tương đương log3 (x – 2)2 + log3 (x – 4)2 = 0
<=> log3 [(x – 2)2(x – 4)2] = 0 <=> (x – 2)2(x – 4)2 = 1 <=> x = 3.
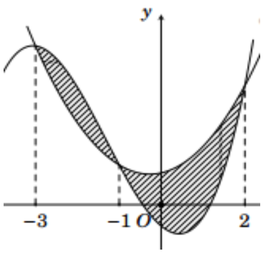
Người ta dự định trồng hoa Lan Ý để trang trí vào phần tô đậm (như hình vẽ). Biết rằng phần tô đậm là diện tích hình phẳng giới hạn bởi hai đồ thị y = f ( x ) = ax 3 + bx 2 + cx - 1 2 và y = g x = dx 2 + ex + 1 trong đó a , b , c , d , e ∈ ℝ Biết rằng hai đồ thị đó cắt nhau tại các điểm có hoành độ lần lượt bằng -3; -1; 2 chi phí trồng hoa là 800000 đồng/1m2 và đơn vị trên các trục được tính là 1 mét. Số tiền trồng hoa gần nhất với số nào sau đây? (làm tròn đến đơn vị nghìn đồng).
A. 4217000 đồng.
B. 2083000 đồng.
C. 422000 đồng.
D. 4220000 đồng.
Một người gửi vào ngân hàng 100 triệu đồng với lãi suất ban đầu 4% một năm và lãi hàng năm được nhập vào vốn. Cứ sau mỗi năm lãi suất tăng 0,3%. Hỏi số năm đầu tiên (kể từ khi bắt đầu gửi tiền) để tổng số tiền người đó nhận được lớn hơn 125 triệu đồng? (làm tròn đến đơn vị nghìn đồng)
A.4 năm
B.5 năm
C.3 năm
D.6 năm
Ngày 27 tháng 3 năm 2016 bà Mai gửi tiết kiệm vào ngân hàng số tiền 100 triệu đồng với hình thức lãi kép và lãi suất 6,8% một năm. Bà Mai dự tính đến ngày 27 tháng 3 năm 2020 thì rút hết tiền ra để lo công chuyện. Hỏi bà sẽ rút được bao nhiêu tiền (làm tròn kết quả đến hàng nghìn)
A. 38949000 đồng
B. 21818000 đồng
C. 31259000 đồng
D. 30102000 đồng
Một bà mẹ Việt Nam anh hùng được hưởng số tiền là 4 triệu đồng trên 1 tháng (chuyển vào tài khoản ngân hàng của mẹ ở ngân hàng vào đầu tháng). Từ tháng 1 năm 2019 mẹ không đi rút tiền mà để lại ngân hàng và được tính lãi 1% trên 1 tháng. Đến đầu tháng 12 năm 2019 mẹ đi rút toàn số tiền ( gồm số tiền của tháng 12 và số tiền gửi từ tháng1). Hỏi khi đó mẹ lĩnh về bao nhiêu tiền? (kết quả làm tròn theo đơn vị nghìn đồng).
A.50970000 đồng
B.50560000 đồng
C.50670000 đồng
D.50730000 đồng
Một chi tiết máy có hình dạng như hình vẽ 1, các kích thước được thể hiện trên hình vẽ 2 (hình chiếu bằng và hình chiếu đứng).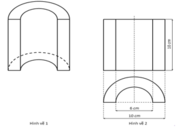
Người ta mạ toàn phần chi tiết này bằng một loại hợp kim chống gỉ. Để mạ 1m2 bề mặt cần số tiền 150000 đồng. Số tiền nhỏ nhất có thể dùng để mạ 10000 chi tiết máy là bao nhiêu? (làm tròn đến hàng đơn vị nghìn đồng).
![]()
![]()
![]()
![]()
Một người gửi 100 triệu đồng vào tài khoản tiết kiệm với lãi suất 0,6%/tháng. Cứ đều đặn sau đúng một tháng kể từ ngày gửi người đó rút ra 500 nghìn đồng. Hỏi sau đúng 36 lần rút tiền, số tiền còn lại trong tài khoản của người đó gần nhất với phương án nào dưới đây? (biết rằng lãi suất không thay đổi và tiền lãi mỗi tháng tính theo số tiền có thực tế trong tài khoản của tháng đó).
A. 104 triệu đồng
B. 106 triệu đồng
C. 102 triệu đồng
D. 108 triệu đồng
Cho phí cho xuất bản x cuốn tạp chí (bao gồm: lương cán bộ công nhan viên giấy in…) được cho bởi C ( x ) = 0 , 0001 x 2 - 0 , 2 x + 10000 , C ( x ) được tính theo đơn vị là vạn đồng. Chi phí phát hành cho mỗi cuốn là 4 nghìn đồng. Tỉ số M(x)=T(x)/x với T(x) là tổng chi phí (xuất bản và phát hành) cho x cuốn tạp chí được gọi là chi phí trung bình cho một cuốn tạp chí khi xuất bản x cuốn. khi chi phí trung bình cho mỗi cuốn tạp chí M(x) thấp nhất tính chi phí cho mỗi cuốn tạp chí đó.
A. 15.000 đồng.
B. 20.000 đồng.
C. 10.000 đồng.
D. 22.000 đồng.
Công ty A nhận định rằng, khi sản xuất x sản phẩm thì giá bán của mỗi sản phẩm là p = 120 - x (nghìn đồng). Biết rằng chi phí sản xuất x sản phẩm là C(x) = x2 + 5x + 300 (nghìn đồng). Hàm lợi nhuận của công ty là:
| A. 2x2 - 115x + 300 | |
| B. 120 x2 - x3 | |
| C. x3 + 5x2 + 300x | |
| D. -2x2 + 115x - 300 |
Một người vay ngân hàng số tiền 400 triệu đồng, mỗi tháng trả góp 10 triệu đồng và lãi suất cho số tiền chưa trả là 1% mỗi tháng. Kỳ trả đầu tiên là cuối tháng thứ nhất. Biết lãi suất không đổi trong suốt quá trình gửi, hỏi số tiền còn phải trả ở kỳ cuối là bao nhiêu để người này hết nợ ngân hàng? (làm tròn đến hàng nghìn).
A.2.921.000
B.3.387.000
C.2.944.000
D.7.084.000